
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Определить средний стаж работников, дисперсию, среднее квадратическое отклонение, коэффициент вариации. Сделать вывод.
С вероятностью 0,997 определить возможные пределы среднего стажа работы по всем работникам банка, а также возможные пределы для доли работников банка, имеющих стаж работы менее 5 лет.
Решение: 1 Для расчетов построим расчетную таблицу 6.
Таблица 6
| Стаж, лет | Число работ., fi | Середина xi | xi*fi | _ (xi – x) | _ (xi – x)2 | _ (xi – x)2*fi |
| До 3 | - 3 | |||||
| 3-5 | - 1 | |||||
| 5-7 | ||||||
| 7-9 | ||||||
| Свыше 9 | ||||||
| Итого | - | - | - |
 |
Средний стаж работников равен
 |
Дисперсия равна
Среднеквадратическое отклонение равно s = Ös2 =
= Ö3,56 = 1,887 лет.
 |
Коэффициент вариации равен
Вывод 1. Средний стаж работы по отобранным работникам составил 5 лет, средний разброс индивидуальных значений стажа работы вокруг средней составил 1,887 года. Так как коэффициент вариации больше 33 %, то распределение работников банка по стажу работы является неоднородным.
2 Определим ошибки выборки. Так как вероятность Р= 0,997, то коэффициент доверия t = 3. Рассчитаем выборочную долю для признака – стаж работы менее 5 лет. Так как данный стаж работы имеют 1 и 2 группы работников в выборке, то w = m/n = (10+48)/100 = 0.58. Дисперсия выборочной доли s2w = w*(1 – w) = 0,58*0,42 =0,2434.
 |
Определим предельную ошибку выборки для среднего по формуле (8).
 |
Определим предельную ошибку выборки для доли по формуле (10).
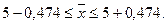 |
Построим доверительный интервал для среднего по формуле (7).
 |
Построим доверительный интервал для выборочной доли по формуле (9).
Вывод 2. С вероятностью 0,997 можно утверждать, что средний стаж работы всех работников банка находится в пределах от 4,526 до 5,474 лет, а доля всех работников банка, имеющих стаж работы менее 5 лет, находится в пределах от 45,6% до 70,4%.
 |
Задачи 4, 5, 6. Предложены на тему"Ряды динамики".При решении задачи 4 необходимо определить средний уровень по моментному ряду динамики. Расчет средних уровней производится по формулам – средней хронологической простой при равноотстоящих уровнях ряда (11)
и по средней хронологической взвешенной при не равноотстоящих уровнях ряда, где ti – расстояние между соседними уровнями ряда, (yi +yi+1)/2 – средняя между соседними уровнями ряда (12).
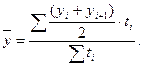 |
Решение типовых примеров на определение средних уровней подробно рассмотрено в [1, с.181-182, 194-196;2, с. 232-233;3, с.51-52].
Для решения задачи 5 необходимо изучить темы "Показатели анализа ряда динамики" и "Методы выявления основной тенденции в ряду динамики" [1, с. 182-188, 191-193;2, с.229-232, 237-240;3, с. 52-59]. Для характеристики интенсивности изменения явления во времени (задание 5.1 и 5.2) необходимо рассчитать следующие показатели: абсолютные приросты, темпы роста и прироста, абсолютное значение 1% прироста, а также средние показатели. Все эти показатели определяются по формулам:
Дата добавления: 2014-12-23; просмотров: 1457; Мы поможем в написании вашей работы!; Нарушение авторских прав |