Здесь в каждой строке (Ф — 1) независимых уравнений, а всего строчек К. Следовательно, имеется К(Ф — 1) уравнений, которые

делают зависимыми (закрепляют, связывают) К(Ф — 1) переменных. Число переменных, которые остались независимыми равно:

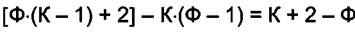
Таким образом, можно произвольно задавать значения К + 2 — Ф переменных не разрушая систему, т.е. не изменяя числа фаз. Число степеней свободы многофазной системы 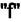равно

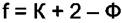(4.2)

Равенство (4.2) называется правилом фаз Гиббса. - это число обобщённых сил 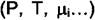, которые можно произвольно менять не

изменяя числа фаз. Число степеней свободы многофазной системы может быть равно 0 или быть положительным. Тогда из (4.2) имеем

>

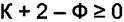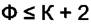
Последнее равенство означает, что в равновесной системе число фаз может превышать число компонент

Нужно более точно определить понятия "компонент" и "фаза". Если в системе не идут реакции, то количество компонент равно числу веществ в системе. Если идут реакции, то число компонент -это минимальное число веществ 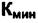, из которых можно построить систему.Поясним это подробнее. Рассматривая многофазную систему, в которой происходят химические превращения, необходимо учитывать также число уравнений, описывающих химические равновесия. Это уравнения связи концентраций реагирующих веществ через константу равновесия и возможные уравнения материального баланса. Эти дополнительные уравнения надо вычесть из правой части уравнения (4.2). Но, чтобы не изменять способа записи правила фаз для многофазных систем без реакций и с реакциями, число компонентов определяют уравнением

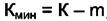
где m - число химических реакций и уравнений материального баланса, 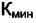- минимальное число веществ, необходимых для построения системы. Тогда правило фаз в виде (4.2) может быть переписано в виде

(4.3)

Уравнение (4.3) можно использовать для многофазных систем, как без реакций, так и при их наличии. В данном случае число компонентов может не совпадать с числом сортов молекул, составляющих систему.

Приведём простой пример.

1)Система задаётся напуском произвольных количестви 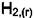. Идёт реакция

, дополнительное уравнение в равновесии Тогда

2) Система задаётся напуском произвольного количества 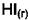. Идёт реакция

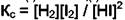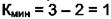. В этом случае появляется два дополнительных уравнения: и уравнение материального баланса 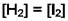т.е. m = 2.Тогда

Фаза - сумма гомогенных частей гетерогенной системы, которые обладают одинаковыми термодинамическими характеристиками и химическим составом и отделёны поверхностью раздела от других фаз.

Максимальное число фаз в равновесной системе реализуется при величине f = 0. В однокомпонентной системе , если К = 2, то

Фмакс = 4.

Если допустить, что один из компонентов отсутствует в одной из фаз,

то это не отразится на числе степеней свободы. Исчезнет одно из

уравнений , но одновременно необходимо ввести условие

отсутствия "i" в фазе Х, т.е. 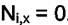. Общее число уравнений при этом

останется неизменным, и правило фаз сохранит свою форму. Например, газовая фаза не содержит солевых компонент.

В случае, если рассматривается система только из конденсированных фаз (ж. или ж. + т.), давление столь слабо влияет на объёмы фаз и распределение компонент по фазам, что это не влияет на превращения в системе. В этом случае правило фаз Гиббса записывается так

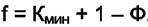(4.4)

Правило фаз неприменимо в критической точке однокомпонентной системы. В критической точке состояние системы характеризуется единственными значениями и 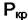и система не имеет степеней свободы, т. е. f = 0. Но при К = 1 из (4.2) следует, что Ф = 3. Для критического состояния очень существенными становятся поверхностные эффекты (σмф→0 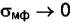при подходе к критической точке) и

не соблюдается второе ограничение на систему, введённое при выводе правила фаз.