
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Степенные средние
Степенные средние: простая  , взвешенная
, взвешенная  ,
,
где х – варианта, т.е. варьирующая, изменяющаяся величина признака; n – число единиц или объем совокупности (число вариантов); f – частота признака (вес I-того варианта); z – показатель степени средней.
Таблица 2.1
Виды степенных средних и формулы их расчёта
| Наименование средней | Условное обозначение | Значение степени | Формула средней | |
| простой | взвешенной | |||
| средняя гармоническая | 
| –1 | 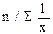
| 
|
| средняя геометрическая | 
| 
| 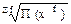
| |
| средняя арифметическая | 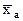
| +1 | 
| 
|
| средняя квадратическая | 
| +2 | 
| 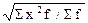
|
«правило мажорантности средних»:  <
< 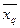 <
<  <
< 
Задача 2.1. На основании исходных данных рассчитать средние и показать «правило мажорантности средних».
Расчетная таблица средних Таблица 2.2
| ∑ | |||||||
| x | |||||||
| 1/x | 0,0185 | 0,0161 | 0,0147 | 0,0135 | 0,0125 | 0,0116 | 0,0870 |
| х² |
средняя гармоническая:  ;
;
средняя геометрическая:  ;
;
средняя арифметическая:  ;
;
средняя квадратическая:  .
.
«правило мажорантности средних»:
 <
< 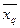 <
<  <
<  68,97 < 69,83 < 70,67 < 71,48
68,97 < 69,83 < 70,67 < 71,48
Вывод: Величина степенных средних зависит от их степени, наибольшее значение имеет
средняя квадратическая (значение степени равно +2).
Задача 2.2. По приведенным данным вычислить среднюю доходную таксу по письменной корреспонденции в целом по группе РУС за 1-е и 2-е полугодие, а также за год.
Исходные данные Таблица 2.3
| РУС | 1-е полугодие | 2-е полугодие | ||
| средняя доходная такса, руб. | количество писем, тыс.ед. | средняя доходная такса, руб. | Сумма доходов тыс. руб. | |
| 23,4 | 28,6 | 31317,0 | ||
| 28,6 | 32,7 | 26977,5 | ||
| 21,9 | 25,2 | 28904,4 | ||
| 24,2 | 29,3 | 27776,4 |
Решение
Расчетная таблица Таблица 2.4
| РУС | 1-е полугодие | 2-е полугодие | Х1*f1 | (М/Х2) | ||
| средняя доходная. такса Х1 | количество писем f1 | средняя доходная. такса . Х2 | сумма доходов тыс. руб. М | |||
| 23,4 | 28,6 | 31317,0 | ||||
| 28,6 | 32,7 | 26977,5 | ||||
| 21,9 | 25,2 | 28904,4 | ||||
| 24,2 | 29,3 | 27776,4 | ||||
| ∑ | 114975,3 | |||||
1-е полугодие используется среднеарифметическая:  руб.
2-е полугодие используется среднегармоническая: руб.
2-е полугодие используется среднегармоническая:  руб.
За год: руб.
За год:  руб. руб.
|
Задача 2.3. На основании исходных данных о заработной плате работников и их количестве рассчитать среднюю величину вариационного ряда с помощью способа "от условного нуля" и традиционным способом.
Таблица 2.5
Исходные данные
| Группа по зарплате тыс. руб. | 10,1 - 13 | 13,1 - 16 | 16,1 - 19 | 16,1 - 19 | 22,1 - 25 | 25,1 - 28 | 28,1 - 31 | 31,1 - 34 |
| Количество работников, чел. |
Таблица 2.6
Расчетная таблица средней
| Группа по зарплате тыс. руб. | Количество работников, чел. | Средняя интервала

| x∙f | 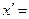 (x-A) / i
A=23,5
(x-A) / i
A=23,5
|

|
| 10,1 - 13 | 11,5 | 80,5 | -4 | -28 | |
| 13,1 - 16 | 14,5 | 130,5 | -3 | -27 | |
| 16,1 - 19 | 17,5 | -2 | -28 | ||
| 19,1 - 22 | 20,5 | 389,5 | -1 | -19 | |
| 22,1 - 25 | 23,5 | ||||
| 25,1 - 28 | 26,5 | 344,5 | |||
| 28,1 - 31 | 29,5 | ||||
| 31,1 - 34 | 32,5 | ||||
| k = i = 3,0 | -61 |
Расчёт средней способом "от условного нуля":
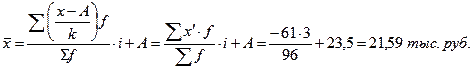 |
Расчёт средней традиционным способом по формуле среднеарифметической взвешанной:
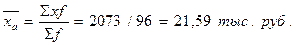
Задача 2.4 На основании исходных данных о количестве работников определить среднее ежегодное изменение работников в %.
Таблица 2.7
Исходные данные
| Показатели | |||||
| Численность работников |
Таблица 2.8
Расчетная таблица
| Численность работников | |||||
| Цепные индексы роста работников | 1,077 | 0,798 | 0,965 | 0,655 |
Используется средняя геометрическая: 
4 ____________________________
√1,077*0,798*0,965*0,655 = 0,8585 = 85,85%
2.2 Структурные средние
Дата добавления: 2014-12-23; просмотров: 322; Мы поможем в написании вашей работы!; Нарушение авторских прав |