КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Расчет моды и медианы.
Задача 2.5. На основании исходных данных о заработной плате работников и их количестве рассчитать моду и медиану.
Таблица 2.9
Исходные данные
| Группа по зарплате тыс. руб. | 10,1 - 13 | 13,1 - 16 | 16,1 - 19 | 19,1 - 22 | 22,1 - 25 | 25,1 - 28 | 28,1 - 31 | 31,1 - 34 |
| Количество работников, чел. |
Мода в интервальном ряду определяется по формуле:
 |
Модальный ряд определяется по наибольшей частоте.





Расчет моды по таблице Таблица 2.10
| Группа по зарплате тыс. руб | Численность работников, чел. |
| 10,1 - 13 | |
| 13,1 - 16 | |
| 16,1 - 19 | |
| 19,1 - 22 | |
| Мо 22,1 - 25 | 22 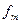
|
| 25,1 - 28 | |
| 28,1 - 31 | |
| 31,1 - 34 | |
| ||||||||
 
| ||||||||

| ||||||||
| ||||||||

| ||||||||
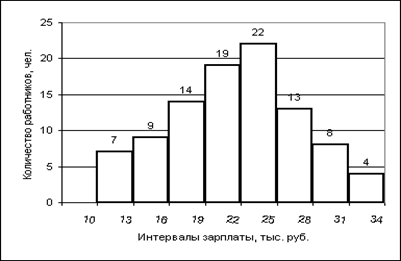
| Рис. 2.1 Гистограмма распределения работников по зарплате (определение моды). |
Медиана в интервальном ряду определяется по формуле:
 |
Медианный ряд определяется по накопленной частоте, ближайшей с большей стороны к  .
.  .
. 


Расчет медианы по таблице Таблица 2.11
| Группа по зарплате тыс. руб | Численность работников, чел. | Численность работников, чел. (накопленные частоты) |
| 10,1 - 13 | ||
| 13,1 - 16 | ||
| 16,1 - 19 | ||
| Ме 19,1 - 22 | ||
| 22,1 - 25 | ||
| 25,1 - 28 | ||
| 28,1 - 31 | ||
| 31,1 - 34 | ||
|
| ||||||||

| 
| |||||||
| ||||||||
| Рис.2.2. Кумулята распределения работников по зарплате (определение медианы). |
На графике при построении кумуляты точки откладываются по верхней границе ординаты.
Тема 3. Показатели вариации
Цель занятия: Ознакомится с различными видами и свойствами показателей вариации, способами их расчета.
Задача 3.1. На основании исходных данных о заработной плате работников и их количестве рассчитать показатели вариации.
В расчетах используются данные, приведенные в таблице 3.1.
1. Размах вариации:
R = xmax – xmin = 34,0 - 10,1 = 23,9 тыс. руб.
2. Среднее линейное отклонение:
 |
3. Дисперсия:
 а) традиционный способ:
а) традиционный способ:
б) способ расчёта от «условного нуля»
 |
в) способ разностей между средней квадратов и квадратом средней:
 |
г) способ моментов:
 |
- Условные моменты:
 | ||||
 | ||||
 |
Расчетная таблица определения дисперсии и условных моментов Таблица 3.1
| Группа по зарплате тыс. руб | Численн. работников, чел. | Средняя интервала

|

| 
| 
| 
| 
| 
| 
| 
|
| 10,1 - 13 | 11,5 | 70,658 | 713,222 | -4 | -28 | -448 | 925,75 | |||
| 13,1 - 16 | 14,5 | 63,846 | 452,924 | -3 | -27 | -243 | 1892,25 | |||
| 16,1 - 19 | 17,5 | 57,316 | 234,652 | -2 | -28 | -112 | 4287,5 | |||
| 19,1 - 22 | 20,5 | 20,786 | 22,740 | -1 | -19 | -19 | 7984,75 | |||
| 22,1 - 25 | 23,5 | 41,932 | 79,922 | 12149,5 | ||||||
| 25,1 - 28 | 26,5 | 63,778 | 312,895 | 9129,25 | ||||||
| 28,1 - 31 | 29,5 | 63,248 | 500,039 | |||||||
| 31,1 - 34 | 32,5 | 43,624 | 475,763 | |||||||
| k = i = 3,0 | 425,188 | 2792,156 | -61 | -637 | 47556,0 |
 5. Среднее квадратическое отклонение:
5. Среднее квадратическое отклонение:
 |
6. Сложение дисперсий
Определение количественных изменений признака по группам, на которые разбита вся совокупность, а также и между группами посредством вычисления и анализа дисперсий: общей, межгрупповой, внутригрупповой и средней из внутригрупповых дисперсий.
Общая дисперсия измеряет вариацию признака во всей совокупности под влиянием всех факторов, обусловливающих эту вариацию:
 .
.
Межгрупповая дисперсияхарактеризует систематическую вариацию, т.е. различия в величине изучаемого признака, возникающие под влиянием признака-фактора, положенного в основание группировки:
 , где
, где
 - соответственно средние и численности по отдельным группам,
- соответственно средние и численности по отдельным группам,
 - средняя всей совокупности.
- средняя всей совокупности.
Внутригрупповая дисперсияотражает случайную вариацию, т.е. часть вариации, происходящую под влиянием неучтенных факторов и не зависящую от признака-фактора, положенного в основу группировки:
 , где
, где
 - варианты групп,
- варианты групп,  - численность группы,
- численность группы,  - средняя группы
- средняя группы
Средняя из внутригрупповых дисперсийопределяется по формуле:
 .
.
Общая дисперсия определяется как сумма средней из внутригрупповых дисперсий и межгрупповой дисперсии:
 .
.
Данная сумма называется правилом сложения дисперсий.
Общая дисперсия, возникает под влиянием всех факторов, равна сумме дисперсий, возникающих под влиянием прочих факторов, и дисперсии, возникающей за счет группировочного признака.
Показатель тесноты связи между группировочным (факторным) и результирующим признаками называется эмпирическим корреляционным отношением и рассчитывается как корень квадратный из отношения межгрупповой дисперсии к общей дисперсии:  .
.
Отношения межгрупповой дисперсии к общей дисперсии называется эмпирическим коэффициентом детерминациии показывает долю группировочного признака в общей вариации:  .
.
Рассчитывается коэффициент вариации по каждой группировки и в целом по всей совокупности: 
Задача 3.2. Объяснить, чем вызвана вариация производительности труда на двух предприятиях с различными группами работников. Вычислить все виды дисперсий. Определить степень влияния разряда работников на производительность труда.
Таблица 3.2
Исходные данные
| Предприятия с работниками | Количество предприятий | Средняя производительность труда, тыс. руб./чел. | Среднее квадратическое отклонение |
| 1-3 го разряда | |||
| 4-6 го разряда |
1. Внутригрупповая дисперсия:  402 = 1600 ;
402 = 1600 ;  302 = 900.
302 = 900.
2. Межгрупповая дисперсия:  =
=  .
.
3. Средняя межгрупповая:  .
.
4. Средняя из внутригрупповых дисперсий: 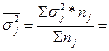

5. Правило сложения дисперсий:общая дисперсия :  .
.
6. Эмпирический коэффициент детерминации: 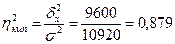 .
.
Вывод: Группировочным признаком обусловлено 87,9% вариации производительности труда от разряда квалификации.
7. Эмпирическое корреляционное отношение:  =
= 
Связь между производительностью труда и разрядом квалификации сильная.
8. Коэффициент вариации по первой группировке: 

коэффициент вариации по второй группировке: 
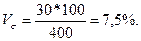
общий коэффициент вариации 

в целом по всей совокупности:
Совокупность каждой группировки можно считать однородной, так как коэффициенты вариации меньше 33%. Общая совокупность не однородная, так как коэффициент вариации больше 33%.
7. Относительные показатели вариации
Задача 3.3. По расчетным данным задач 2.3 и 3.1 (средняя величина =21,594, размах вариации = 23,9, среднее линейное отклонение = 4,429, среднее квадратическое отклонение = 5,393) рассчитать относительные показатели вариации.
 |
1. Коэффициент осцилляции:
 |
2. Линейный коэффициент вариации:
 |
3. Коэффициент вариации:
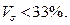 Совокупность можно считать однородной, т. к.
Совокупность можно считать однородной, т. к.
8. Расчет асимметрии и эксцесса.
1. Асимметрия:  а)
а) 
б) 
в) 
Центральный момент третьего порядка: m3 = (m3 – 3m1 m2 + 2m13)·i3 =
[(-6,6354)-3∙( -0,6354) ∙3,6354+2 ∙ (-0,6354³)] ∙3³ = -5,904
Вывод: асимметрия левосторонняя, слабосмещенная.
2. Эксцесс: 
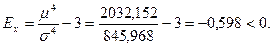
Центральный момент четвёртого порядка: m4 = (m4 – 4m3 m1 + 6m2m12 - 3m14)·i4
[33,6354 – 4*(-6,6354)*(-0,6354) + 6*3,6354*(-0,63542) - 3*(-0,63544)]*34 = 2032,152.
 Вывод: низковершинное распределение.
Вывод: низковершинное распределение.
Дата добавления: 2014-12-23; просмотров: 317; Мы поможем в написании вашей работы!; Нарушение авторских прав |