Тема 5. Выборочное наблюдение

Цель занятия: Ознакомится с различными видами и способами выборочного наблюдения, а также показателями, характеризующими репрезентативность выборки.

Основные формулы для расчета показателей, характеризующих

выборочную совокупность Таблица 5.1

Показатели	обозначение	Способ выборки
Повторный	бесповторный
Средняя ошибка выборки - для количественного признака     - для доли	µх µw	или
Предельная ошибка выборки - для количественного признака - для доли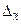
Относительная ошибка выборки - для количественного признака   - для доли	βх βw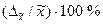
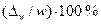
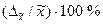
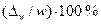
Необходимый объём выборки - для количественного признака - для доли	nx nw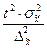

Задача 5.1. Выборочное обследование длительности междугородных телефонных соединений дало следующее распределение:

Вычислить: среднюю длительность соединения; среднюю, предельную и относительную ошибки данной выборки с вероятностью ρ = 0,997. Выборка повторная.

Решение

Расчетная таблица Таблица 5.2

									∑
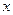
	740,6	202,8	25,2	39,2	173,4	437,4	547,6	441,8

Средняя длительность соединения: 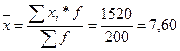мин.

Средняя ошибка выборки при повторной выборке:

дисперсия: , .

Предельная ошибки выборки: D = t*m,

при ρ = 0,997 t = 3 D = 3*0,255 = 0,765 мин.

Относительная ошибки выборки: %, .

Доверительные интервалы для генеральной средней:

(от 6,835 до 8,365).

Задача 5.2. По данным о междугородных телефонных соединениях, предоставленных с ожиданием свыше 1 часа, определить:

- долю соединений, предоставленных с ожиданием свыше 1 часа;

- ошибку данной выборки с вероятностью ρ = 0,95.

Выборка бесповторная.

Генеральная совокупность междугородных телефонных соединений 1250 ед.

Выборочная совокупность 570 ед., в том числе с ожиданием свыше 1 часа 45 ед.

Решение

Определяется доля единиц, обладающая признаком (с ожиданием свыше 1 часа):

W = m / n W = 45 / 570 = 0,079 или 7,9 %.

Определяется предельная ошибка выборочной доли при бесповторной выборке:

, при ρ = 0,95 t = 2.

или 1,66%

Пределы доли признака в генеральной совокупности:

, т.е. в пределах от 6,56 до 9,56%.

Определяется относительная ошибка выборочной доли: %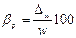

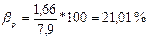. Относительная ошибка выборочной доли велика, значит объем выборочной совокупности недостаточен.

Задача 5.3 Сколько работников надо обследовать в порядке случайной выборки для определения средней заработной платы, чтобы с вероятностью ρ = 0,955 можно было бы гарантировать ошибку не более 50 руб., если среднее квадратическое отклонение зарплаты – 200 руб. Выборка повторная. При ρ = 0,955 t = 2.

Определить объем выборки, если ошибку выборки а) увеличить в 2 раза, в) уменьшить в 2 раза.

Решениее

Для случайного повторного отбора: ; чел.

а) если ошибку выборки увеличить в 2 раза: чел.

в) если ошибку выборки уменьшить в 2 раза: чел.

Вывод: Необходимо обследовать 64 чел. При увеличении ошибки выборки в 2 раза объем выборки уменьшается в 4 раза, при уменьшении ошибки выборки в 2 раза объем выборки увеличивается в 4 раза, т. е. происходит изменение в квадрат раз.