Определения близости эмперического и теоретического распределений

Под выравниванием вариационных рядов понимается подбор теоретического распределения, близкого к фактическому (эмпирическому) распределению и определение существенности расхождения между ними с использованием критериев согласия (Колмогорова, Пирсона, Романовского).

В основу теоретического распределения положено нормальное распределение, которое описывается формулой:

,

где: Y – ордината кривой нормального распределения;

- нормальные отклонения, т.е. отклонения вариантов от , выраженные в единицах среднего квадратического отклонения σ.

-3σ -2σ - σ + σ +2σ -3σ

Рис. 4.3 Кривая нормального распределения

При выравнивании вариационного ряда по кривой нормального распределения теоретические частоты ряда определяются по формуле:

,

где: N = ∑f - сумма всех частот вариационного ряда;

h = i – величина интервала в группах;

- постоянный множитель, характеризующий данный вариационный ряд.

Величина (значение функции) табулирована.

Задача 4.9. По имеющимся данным о количестве работников компании и их заработной плате определить эмпирическое и теоретическое распределения и определение существенности расхождения между ними с использованием критериев согласия (Колмогорова, Пирсона, Романовского).

Таблица 3.3

Расчетная таблица определения близости эмперического и теоретического распределений

Группа по зарплате тыс. руб	Численн. работников, чел.	Средняя интервала			f(t)	φ(t)	Кумулятивные частоты   фактич. теоретич. ∑φ ∑f	Разность ∑f -­ ∑φ
10,1 - 13		11,5	-10,094	-1,87	0,0694	3,7		3,7	3,3
13,1 - 16		14,5	-7,094	-1,32	0,1669	8,9		12,6	D 3,4
16,1 - 19		17,5	-4,094	-0,76	0,2989	16,0		28,6	1,4
19,1 - 22		20,5	-1,094	-0,20	0,3910	20,9		49,5	-0,5
22,1 - 25		23,5	1,906	0,35	0,3752	20,0		69,5	1,5
25,1 - 28		26,5	4,906	0,91	0,2637	14,1		83,6	0,4
28,1 - 31		29,5	7,906	1,47	0,1354	7,2		90,8	1,2
31,1 - 34		32,5	10,906	2,02	0,0519	2,8		93,6	2,4
k = i = 3,0						93,6

продолжение таблицы

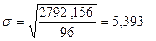Группа по зарплате тыс. руб	Число работников fТ	fэ – fТ	(fэ – fТ)² / fТ
10,1 - 13			2,25	713,222
13,1 - 16				452,924
16,1 - 19		-2	0,25	234,652
19,1 - 22		-2	0,190	22,740
22,1 - 25			0,2	79,922
25,1 - 28		-1	0,071	312,895
28,1 - 31			0,143	500,039
31,1 - 34			0,333	475,763
			3,438	2792,156

Решение

1. Расчёт средней заработной платы:

2. Расчёт среднеквадратического отклонения:

.

3. Расчет теоретических частот ряда :

4. Расчет критерия согласия.

КритерийКолмогорова ( ):

По таблице значений P(λ) P(λ=0,347)=0,9997

С вероятностью 99,97% можно утверждать, что расхождения между эмпирическим (фактическим) и теоретическим распределением имеют случайный характер.

находится по таблице, близко к 1,0.

Вывод: расхождения между эмпирическим и теоретическим рядами распределения не существенны и носят случайный характер.

Рис. 4.4 Эмпирический и теоретический ряды распределения

Критерий Пирсона ( )("хи-квадрат") :.

Условие близости эмпирического и теоретического распределений:

При v = h-3 = 8-3 = 5 и α = 0,05 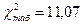. V - число степеней свободы,

h- число групп ряда, α – уровень значимости.

Если , значит различия не существенны.

По таблице «Значения - критерия Пирсона при полученных значениях

число степеней свободы Уровень значимости принимаем α = 0,05 ; m - число групп; n - число параметров.

Критерий Романовского: .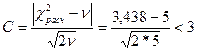

ЕслиC< 3, значит различия не существенны.

Правило 3-х :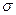

Критерии согласия могут определить зону для нормального распределения эмпирического ряда распределения:

21,59 + 5,39 = 26,98 21,59 - 5,39 = 16,2;

21,59 + 2*5,39 = 32,37 21,59 - 2*5,39 = 10,81;

21,5 + 3* 5,39 = 37,76 21,5 - 3* 5,39 = 5,42.

В пределах границ находятся частоты:

от 16,20 до 26,98 (22+19) = 41 41/96 = 42,7%;

от 10,81 до 32,37 (41+14+13+) = 68 68/96 = 70,8%;

от 5,42 до 37,76 (68+7+9+8) = 92 92/96 = 95,8%.

Таким образом, большинство частот эмпирического ряда распределения (95,8%) находятся в пределах 3-х σ.