Основные теоретические сведения. В общем случае регрессия – функциональная зависимость между объясняющими переменными Хj и объясняемой переменной Y

В общем случае регрессия – функциональная зависимость между объясняющими переменными Х_j и объясняемой переменной Y, которая строится с целью прогнозирования среднего значения Y при заданных значениях Х_j =x_j, или для анализа влияния отдельных переменных Х_j, на зависимую переменную.

Различают уравнения регрессии I и II рода.

Уравнением регрессии первого рода называют уравнение вида

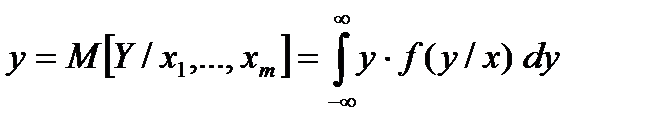. (1.1)

Если уравнение (1.1) представляет собой уравнение связи двух случайных величин Y и Х, то это уравнение представляет собой уравнение парной регрессии. В предположении нормального распределения случайной величины (Y, Х) парную регрессию называют линейной парной регрессией, т.к. в этом случае условное математическое ожидание (1.1) представляет собой уравнение прямой линии

Y = M (Y/x) = ₀ + ₁ Х . (1.2)

Для точного описания уравнения регрессии необходимо знать условный закон распределения зависимой переменной Y при условии, что переменная Х примет значение х. В связи с тем, что реальные значения переменной Y не всегда совпадают с ее средним значением M (Y/x), то в уравнение регрессии вводится случайная составляющая . Тогда уравнение (1.2) можно записать в виде

Y^* = M (Y/x) + (1.3)

или для конкретных наблюдений (у_i , x_i )

= ₀ + ₁ x_i + _i , . (1.4)

Уравнение (1.4) называют теоретической линейной моделью.

Возмущения _i , должны удовлетворять основным предпосылкам регрессионного анализа:

1. Математическое ожидание возмущения _i равно нулю

или

₀ + ₁ x_i .

2. Дисперсия возмущения _i постоянна для любого i, т.е.

, .

3. Возмущения _i и _j являются независимыми друг от друга, что влечет за собой отсутствие автокорреляции

.

4. Возмущения _i представляет собой нормально распределенную случайную величину.

Обычно исследователь имеет дело с исходными данными выборки объемом n, где каждое наблюдение – есть точка (Y, Х) в (m+1) – мерном пространстве. Здесь m – число объясняющих переменных.

В случае парной регрессии имеется выборка объемом n двумерной случайной величины (Y, Х).

Уравнением регрессии второго рода называют эмпирическое уравнение регрессии, которое строится на основе данных выборки.

Рассматривается парная линейная регрессия, когда уравнение регрессии второго рода имеет вид

_i = М[Y/X=x] = b₀ + b₁ x_i , . (1.5)

С учетом уравнения (1.3) эмпирическую линейную модель связи переменных Y и Х запишем в виде

= b ₀ + b ₁ x_i + e_i , (1.6)

где , b₀ , b₁ , e _i – оценки соответственно y_i, ₀, ₁, _i .

Построение уравнения регрессии начинается с построения корреляционного поля, представляющего собой графическую зависимость в виде точек случайной величины (Y, Х) на плоскости y0x. По расположению эмпирических точек делается вывод о наличии линейной корреляционной зависимости между переменными Y и Х. Дальнейшее построение уравнения регрессии сводится к оценке ее параметров, используя метод наименьших квадратов (МНК). В этом случае неизвестные параметры b₀ и b₁ выбираются так, чтобы сумма квадратов отклонений эмпирических значений y_i от значений , найденных по уравнению регрессии (1.5), была минимальной

Применение МНК обусловлено тем, что он позволяет получить несмещенные оценки с минимальной дисперсией, в условиях, когда _i удовлетворяют всем предпосылкам регрессионного анализа.

В результате операции МНК оценка выборочного коэффициента регрессии b₁ определяется выражением

b₁ = Cov (X,Y) / , (1.7)

а коэффициента b₀

b₀ = 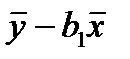, (1.8)

где = у_i /n; = х_i /n; Cov (X,Y) = ; = .

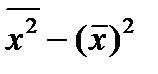Точность оценок коэффициентов линейного уравнения регрессии первого рода характеризуется их выборочными дисперсиями, которые вычисляются по формулам

, (1.9)

. (1.10)

Здесь S² – дисперсия регрессии – оценка дисперсии 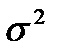, определяемая по формулам

S² = е_i² /(n – 2), е_i = y_i - b₀ - b₁ x_i .

Проверка качества уравнения регрессии осуществляется по ряду позиций.