Оценка статистической значимости коэффициентов регрессии.

Заключается в проверке основной гипотезы Н0 о значимости отличия коэффициентов b0 и b1 от нуля. С этой целью используется критерий Стьюдента. Вычисляются , и сравниваются с tкрит . Результатом сравнения является вывод о значимости коэффициентов b0 и b1 .

2. Интервальные оценки коэффициентов регрессии. Так как объем выборки ограничен, то b₀ и b₁ – случайные величины, поэтому желательно найти доверительные интервалы для истинных значений ₀ , ₁. Для этого также используется статистика

, i = 0,1,

которая имеет t – распределение Стьюдента с степенями свободы. Интервальные оценки параметров _i при заданном уровне значимости имеют вид

, i = 0,1,

с надежностью р = 1- . Здесь t_крит – критическое значение распределения Стьюдента, взятое из таблицы с параметрами и /2.

3. Проверка значимости уравнения регрессии в целом. Позволяет установить, соответствует ли математическая модель экспериментальным данным и достаточно ли включенных в уравнение объясняющих переменных для описания зависимой переменной. Проверка значимости уравнения регрессии производится на основе дисперсионного анализа. Мерой общего качества уравнения регрессии является коэффициент детерминации R²

R² = 1 - е_i² / ( y_i - )² . (1.11)

Выражение (1.11) вытекает из соотношения

( y_i - )² = k_i² + e_i² , (1.12)

где k_i² = – объясненная регрессией сумма квадратов, характеризует разброс, обусловленный регрессией;

e_i² = – остаточная (необъясненная) сумма квадратов, характеризует случайную составляющую разброса y_i относительно линии регрессии .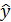

Из соотношений (1.11) и (1.12) следует, что коэффициент детерминации R² есть не что иное, как

R² = k_i² / ( y_i - )². (1.13)

Таким образом, коэффициент детерминации можно вычислить по формулам (1.11) или по (1.13).

Основная цель использования уравнения регрессии – прогноз значений зависимой переменной.

Здесь речь идет о возможных значениях Y_р при определенных значениях объясняющей переменной Х_р. Так как задача решается в условиях неопределенности то прогноз удобнее всего давать на основе интервальных оценок, построенных с заданной надежностью .

Причем здесь возможно два подхода: 1) предсказание среднего значения, т.е. M (Y/ Х=x_р); 2) предсказание индивидуальных значений Y/ Х=x_р .

Интервальный прогноз для среднего значения вычисляется следующим образом:

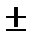t_кр S , (1.14)

где = b₀ + b₁x_р; t_кр – критическое значение, полученное по распределению Стьюдента при количестве степеней свободы = n – 2 и заданной вероятности /2.

Интервальный прогноз для индивидуального значения вычисляется по формуле

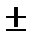t_кр S . (1.15)