Простейшие методы прогнозирования

Наиболее простыми методами прогнозирования по одномерным временным рядам, являются:

· прогнозирование в предложении абсолютной неизменности

значений предшествующих уровней в будущем;

· метод среднего уровня ряда;

· метод среднего абсолютного прироста;

· метод среднего темпа роста.

Рассмотрим каждый из названных методов.

Прогнозирование в предположении абсолютной неизменности значений предшествующих уровней исходит из утверждения, что каждое следующее прогнозное значение будет равно предыдущему значению признака, то есть:

(14.1)

…

где - прогнозное значение на период

упреждения L.

- прогнозное значение предшествующее

периоду упреждения L.

Данный случай прогнозирования является частным и в практике статистического прогнозирования социально-экономических явлений встречается крайне редко.

Другим простейшим методом прогнозирования социально-экономических явлений является метод прогнозирования на основе среднего уровня ряда.

Данный метод прогнозирования используется для случаев, когда изменение значений уровней временных рядов носит стационарный характер.

При построении прогноза данным методом используется принцип, согласно которому значения всех последующих прогнозируемых уровней принимаются равными среднему значению уровней ряда в прошлом, то есть:

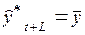(14.2)

Таким образом получают точечный прогноз.

Однако, рассматривая временный ряд как выборку из некоторой генеральной совокупности, сложно предположить, что прогнозная точечная оценка полностью совпадает с эмпирическими значениями признака. В этом случае целесообразно определить доверительный интервал прогноза путем построения интервального прогноза данным методом по выражению вида:

, (14.3)

где t_a - табличное значение t – критерия Стьюдента с (n-1)

числом степеней свободы и уровнем значимости a;

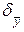- средняя квадратическая ошибка средней, которая

определяется по формуле:

, (14.4)

где - среднее квадратическое отклонение, которое

определяется как:

, (14.5)

где - эмпирические значения уровней временного ряда;

- средний уровень исходного временного ряда;

n – число уровней ряда.

Полученный таким образом доверительный интервал учитывает колеблемость выборочных средних и предполагает, что каждая следующая прогнозная оценка будет равна среднему уровню ряда динамики. При этом упускается из вида возможность колеблемости эмпирических значений признака вокруг средней, то есть в определении доверительного интервала, в расчете дисперсии необходимо учесть как колеблемость выборочных средних, так и степень варьирования индивидуальных эмпирических значений признака вокруг средней.

В этом случае доверительный интервал прогнозной оценки можно определить по выражению вида:

. (14.6)

Как видно, общая вариация прогнозируемого социально-экономического явления, то есть его ошибка, определяется суммой двух дисперсий: общая дисперсия и дисперсия выборочной средней при условии рассмотрения исходного временного ряда как выборки из некоторой генеральной совокупности.

Прогнозирование методом среднего абсолютного прироста предполагает, что общая тенденция развития изучаемого социально-экономического явления наилучшим образом аппроксимируется линейной формой аналитического выражения.

Применение данного метода прогнозирования возможно при предварительной проверке следующих предпосылок:

1.Абсолютные цепные приросты (D_iy = y_i – y_i-1, где y_i - значение уровня i-го периода; y_i-1 - значение уровня предшествующего i-му периоду времени) должны быть приблизительно одинаковыми;

2.Должно выполняться неравенство вида:

,

где - остаточная дисперсия, определяемая по формуле:

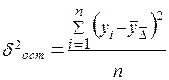, (14.7)

где y_i - эмпирические значения уровней ряда динамики;

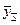- теоретические значения уровней ряда, выравненные

методом среднего абсолютного прироста.

n – число уровней исходного ряда динамики.

, (14.8)

где D_i - цепные абсолютные приросты уровней исходного временного ряда.

После проверки и подтверждения выполнения данной предпосылки можно приступать к прогнозированию методом среднего абсолютного прироста, общая модель прогноза которого имеет вид:

, (14.9)

где - последний уровень исходного ряда динамики

(для перспективного прогноза) или уровень

принятый за базу экстраполяции;

L - период упреждения прогноза;

- средний абсолютный прирост, который определяется

по формулам вида:

или , (14.10)

где - последний уровень исходного ряда динамики;

- первый уровень исходного ряда динамики.

Как видно из приведенных преобразований, прогнозирование методом среднего абсолютного прироста заключается в непрерывном увеличении последнего уровня исходного ряда динамики на величину среднего абсолютного прироста на всем периоде упреждения.

Прогнозирование методом среднего темпа роста осуществляется в случае если темпы роста цепные, рассчитанные по данным исходного ряда динамики за исследуемый период времени, имеют приблизительно одинаковое цифровое значение, а тенденция развития явления подчиняется геометрической прогрессии и может быть описана показательной (экспоненциальной) кривой.

Модель прогноза методом среднего темпа роста имеет вид:

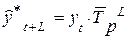, (14.11)

где - последний уровень исходного ряда динамики (для

перспективного прогноза) или уровень принятый за базу

экстраполяции (во всех остальных случаях);

- средний темп роста, который определяется по

формулам вида:

или , (14.12)

где - последний уровень исходного ряда динамики;

- первый уровень исходного ряда динамики;

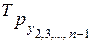- цепные темпы роста;

- произведение цепных темпов роста

Сумма теоретических значений , полученных в результате выравнивания по среднему темпу роста, должна совпадать с суммой эмпирических значений исходного временного ряда :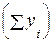

(14.13)

Несовпадение данных сумм может быть вызвано следующими причинами:

1.исходному временному ряду свойственна другая закономерность, а не экспоненциальная;

2.существенное и значимое влияние на изучаемое социально-экономическое явление оказывают случайные факторы.

Рассмотренные методы прогнозирования являются простейшими и поэтому, прогнозы полученные на их основе являются приближенными и не всегда надежны при увеличении периода упреждения. Как правило, эти методы используются только при краткосрочном прогнозировании.

Применение этих методов в среднесрочном и долгосрочном прогнозировании нецелесообразно, так как они не только не учитывают вариацию, скачки внутри временного ряда, но и в основе построения их моделей прогноза и получения прогнозных оценок на всем периоде упреждения лежит принцип равномерного увеличения или уменьшения (в зависимости от знака абсолютного прироста или допустимых границ темпа роста) исследуемого явления, в частности его последнего уровня в исходном временном ряду, от одного периода упреждения к другому на постоянную величину, количественно выраженную значением среднего абсолютного прироста или среднего темпа роста.