Модели сезонных колебаний

Моделью периодически изменяющихся уровней служит ряд Фурье:

, (12.3)

где k — определяет номер гармоники ряда Фурье и может быть

взята с разной степенью точности (чаще от ‘‘1’’ до ‘‘4’’).

Параметры уравнения определяются методом наименьших квадратов, то есть по условию . Решая систему нормальных уравнений, получим:

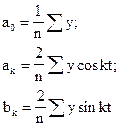. (12.4)

Для изучения сезонности берется (n = 12) по числу месяцев в году.

Как правило, при выравнивании по ряду Фурье рассчитывают не более четырех гармоник и затем уже определяют, какая гармоника наилучшим образом отражает периодичность изменения уровней ряда.

Так, при k=1: ;

k=2: . (12.5)

Рассчитав остаточные дисперсии 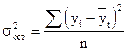для 2-х случаев, можно сделать вывод, какая гармоника Фурье наиболее близка к фактическим уровням ряда.

Моделирование сезонности проводится в следующей последовательности:

1. Определяется тенденция исходного ряда динамики и ее аналитическое выражение, например, в виде линейного тренда:

.

2. Определяются - теоретические уровни ряда динамики;

3. Определяется ( ) - по месяцам года.

4. Определяются средние арифметические по месяцам года. Получается ряд индексов, характеризующих сезонную волну.

6. Определяется модель сезонной волны:

- ряд Фурье.

- порядковый номер гармонии.

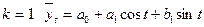
Таблица 12.1

Множители гармонического анализа n=12

для расчета коэффициентов и

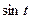
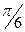
	0,866	0,5		-0,5	0,5	0,866		0,866
	0,5	-0,5	-1	-0,5	0,866	0,866		-0,866
		-1					-1
	-0,5	-0,5		-0,5	0,866	-0,866		0,866
	-0,866	0,5		-0,5	0,5	-0,866		-0,866
	-1		-1
	-0,866	0,5		-0,5	-0,5	0,866	-1	0,866
	-0,5	-0,5		-0,5	-0,866	0,866		-0,866
		-1			-1
	0,5	-0,5	-1	-0,5	-0,866	-0,866		0,866
	0,866	0,5		-0,5	-0,5	-0,866	-1	0,866

- остатки от линейной тенденции.