Проблема автокорреляции в анализе бизнес-процессов

Метод наименьших квадратов, используемый в регрессионном анализе для определения коэффициентов регрессии, основывается на предпосылке независимости друг от друга отдельных наблюдений одной и той же переменной. В динамических же рядах существует еще и автокорреляция. Поэтому величина коэффициентов регрессии, полученных по способу наименьших квадратов, не имеет нужных статистических свойств. Наличие автокорреляции приводит к искажению средних квадратических ошибок коэффициентов регрессии, что в свою очередь затрудняет построение доверительных интервалов по ним и проверку их значимости по соответствующим критериям. Автокорреляция также может привести к сокращению числа наблюдений ввиду невозможности потерять показатели одного и того же объекта за ряд лет, поскольку наблюдение одного объекта за десять лет качественно отличается от наблюдений десяти объектов за одно и то же время. Возникает автокорреляция и в отклонениях от трендов, а также в случайных остатках уравнений регрессии, построенных по многомерным рядам динамики.

Автокорреляция — это наличие сильной корреляционной зависимости между последовательными уровнями временного ряда.

Автокорреляция может быть следствием следующих причин:

· Не учтен в модели существенный фактор, при этом его влияние отражается на величине отклонений, которые в этом случае показывают закономерность в изменении, связанную с изменением неучтенного фактора.

· В модели не учитывается несколько факторов, влияние каждого из которых в отдельности не существенно, но при совпадении изменений этих факторов по направлению и по фазе в отклонениях может возникнуть автокорреляция.

· Автокорреляция в отклонениях может появиться в случае, когда

неправильно выбрана форма связи между y и x.

· Неверно выбран порядок авторегрессионой модели.

· Вследствие специфичности внутренней структуры случайного

компонента.

Прежде чем делать вывод о тесноте связи между рассматриваемыми рядами динамики, необходимо проверять наличие автокорреляции в них, чтобы оценить степень зависимости между соседними уровнями временного ряда.

Наличие автокорреляции устанавливается с помощью коэффициента автокорреляции, который определяется на основе формулы коэффициента корреляции для парной (линейной) связи между уровнями исходного ряда и того же ряда, но сдвинутого на t шагов во времени:

, (13.1)

где y_t — эмпирические значения уровней ряда;

y_t+1 — эмпирические значения уровней, сдвинутые на один

период времени (t = 1).

Возникает проблема заполнения последнего уровня ряда y_t+1. В данном случае возможны два варианта:

1. Если значение последнего уровня мало отличается от первого, то чтобы ряд не укорачивался, его можно условно дополнить . Тогда

(13.2)

И коэффициент автокорреляции будет равен:

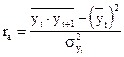или (13.3)

, (13.4)

где . (13.5)

Затем аналогично рассчитывается коэффициент автокорреляции для всех временных рядов, входящих в связный.

Если r_a > r_{a кр} при заданном уровне значимости a и n, то в исходном временном ряду существует автокорреляция, в противном случае она отсутствует.

Последовательность значений коэффициентов автокорреляции r_t, вычисленных при t = 1, 2, ..., l, называют автокорреляционной функцией. Эта функция дает представление о внутренней структуре изучаемого экономического явления.

Для проверки автокорреляции в уровнях ряда также используется и критерий Дарбина-Уотсона. Гипотеза о наличии автокорреляции проверяется с помощью случайной величины:

(13.6)

0 £ d £ 4.

Если автокорреляции в ряду нет, то значения критерия d колеблются вокруг 2.

Эмпирическое значение d сравнивается с табличным значением.

В таблице есть два значения критерия — d₁ и d₂, v и n,

где d₁ и d₂ — нижняя и верхняя границы теоретических

значений;

v — число факторов в модели.

n — число членов временного ряда.

Если 1) d < d₁ — в ряду есть автокорреляция;

2) d > d₂ — автокорреляции нет;

3) d₁ £ d £ d₂ — необходимо дальше исследовать

автокорреляцию.

Иногда приходится при анализе рядов динамики исследовать вопрос о наличии или отсутствии автокорреляции не между самими уровнями ряда, а между их отклонениями от среднего уровня или от выровненного уровня.

При значении r_a £ 0,3 необходимо проверять наличие автокорреляции в остатках с помощью следующего коэффициента Дарбина-Уотсона для остаточных величин:

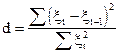, (13.7)

где x_t — отклонения эмпирических значений уровней от

теоретических, полученных по уравнению тренда.

Существует теоретическое распределение значений d_p для положительной автокорреляции с вероятностью 0,95,

где d₁ и d₂ — нижняя и верхняя границы теоретических значений.

n — число факторов в модели;

n — число членов временного ряда.

При применении критерия Дарбина-Уотсона расчетное значение d_p сравнивается с табличными d₁ и d₂. При этом возникает три исхода:

1) d < d₁ => вывод о наличии автокорреляции в отклонениях;

2) d > d₂ => вывод об отсутствии автокорреляции;

3) d₁ £ d £ d₂ => необходимо дальше исследовать автокорреляцию.

Возможные значения критерия находятся 0 £ d £ 4. Они различны для положительной и отрицательной автокорреляции. Так как при отрицательной автокорреляции d Î [2; 4], для проверки следует определять величину (4 - d).

Если в рядах динамики или в остаточных величинах имеется автокорреляция, то оценки коэффициентов регрессии, полученные методом наименьших квадратов, будут несмещенными, но неэффективными, так как наличие автокорреляции увеличивает дисперсии коэффициентов регрессии. Это затрудняет построение доверительных интервалов для коэффициентов регрессии и проверку их значимости.

Из этого следует сделать вывод, что прежде чем проводить корреляционно-регрессионый анализ временных рядов, необходимо исключить из исследуемых рядов автокорреляцию.

После того как установлено наличие автокорреляции следует приступить к построению модели.