Концепция моделирования состояний

Неклассические представления о характеристиках объектов и состояний.

Понятия физической реальности как модели природы подразделяются на два класса. В один входят понятия, описывающие непосредственно исследуемый объект. Это его характеристики, или физические величины, которые в принципе можно измерить в эксперименте (например, координата, импульс, заряд, спин и т.д.).

Другой класс понятий физической реальности составляют характеристики окружения, которое как бы приготавливает объект для рассмотрения в данной ситуации, преподносит его исследователю в некотором виде. Про эти характеристики говорят, что они задают состояние объекта.

Согласно идее Планка, универсальной количественной характеристикой минимального квантового воздействия на объекты, находящиеся в микросостояниях, в природе служит постоянная Планка 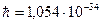Дж×с, или элементарный квант действия. Любое воздействие, происходящее в природе, можно охарактеризовать целым числом квантов действия , так что постоянная Планка играет роль неделимой более «порции» или «атома» воздействия. Поскольку она очень мала, атомизм воздействия, как и всякий другой атомизм, в макроскопических опытах себя не проявляет, что согласуется с наблюдаемой непрерывностью воздействия в классической физике.

К настоящему времени идея Планка обоснована бесчисленными опытами с самыми различными объектами в микросостояниях, из которых следует одно и то же значение 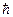. Они подтвердили универсальный характер постоянной Планка, характеризующей не какое-то конкретное микросостояние объекта или конкретное воздействие (включая наблюдение), а фундаментальный закон природы – дискретность, «атомизм» всякого воздействия. В этом смысле постоянная Планка 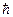– столь же фундаментальная физическая величина, что и скорость света в вакууме с, значение которой также характеризует не просто скорость какого-то конкретного физического процесса, а фундаментальный закон природы – существование универсального ограничения на скорость любого материального объекта.

Универсальный характер постоянной Планка проявляется и в том, что через нее могут быть выражены любые физические характеристики, которыми обмениваются два взаимодействующих объекта (из которых один обязательно микроскопичен). Действительно, размерность элементарного кванта действия такова:

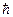[ ]= [энергия ´ время] = [импульс ´ расстояние] = [момент] (3.5),

Поскольку время и расстояние в микромире остаются непрерывными, отсюда непосредственно следует представление о дискретности, квантованности энергии, импульса и момента, передаваемых при взаимодействии.

Микросостояние одной микрочастицы.

Дж. Улленбек и С. Гаудсмит (1925г.) высказали смелую гипотезу, согласно которой электрон все же обладает собственным моментом, но имеющим чисто квантовую природу. Они его назвали спином и предположили, что спин электрона способен иметь только два возможных значения проекци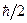и – и (- 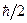) на выделенную ось. Дальнейшее развитие физики показало, что понятие спина, величина которого определяется постоянной Планка, свойственно всем микрочастицам. Оно является для них столь же фундаментальным, как и понятия массы и заряда, и его следует воспринимать как исходное, внутренне присущее им качество, не связанное с каким-либо «вращением» материального объекта вокруг оси. В то же время какое-то отношение к повороту вокруг оси в пространстве спин электрона и других микрочастиц все же имеет. Но все равно это не классическое, а специфически квантовое свойство природы, ибо это – «поворот» квантоводинамических состояний.

Для исследования спина электрона и его проекций необходимо, прежде всего, научиться их «выделять» в чистом виде. Здесь решающую роль играет то обстоятельство, что электрон – заряженная микрочастица, так что с его спином неразрывно связан собственный магнитный момент. Если направление внешнего магнитного поля принято за ось Z, то из опыта следует, что проекции магнитного момента электрона на эту ось принимают два значения

(3.6),

где – проекции спина электрона. Наглядно это можно представить так, как будто с электроном связана «магнитная стрелка». В отсутствие магнитного поля способность ее к ориентации ни в чем себя не проявляет. Однако при наличии магнитного поля она ориентируется только двумя способами – либо по магнитному полю, либо против него, что и позволяет различить два значения проекции спина электрона.

Впервые контуры такого описания наметились при изучении свойств электромагнитного излучения, в частности, света. Дело в том, что в классической физике к описанию свойств света успешно применялись обе модели – корпускулярная и континуальная (волновая). Некоторые свойства света (прямолинейное распространение, отражение и преломление, отклонение в поле тяготения) проще описываются в корпускулярной модели, тогда как другие (интерференция, дифракция, поляризация) в континуальной модели. Из классической теории электромагнетизма Максвелла следовало, что свет и другие электромагнитные излучения способны переносить любые, сколь угодно малые доли энергии, импульса и момента. Однако, если бы это было в действительности так, мы не могли бы наблюдать удаленные звезды, поскольку плотность переносимой энергии света (или его интенсивность) должна по теории Максвелла убывать обратно пропорционально квадрату расстояния. В этом случае до наблюдателя доходила бы малая доля энергии, которая оказалась бы значительно ниже порога чувствительности любого регистрирующего прибора. Тот факт, что звезды все же наблюдаются, служит прямым указанием на то, что энергия света не всегда зависит от интенсивности волны и поэтому с расстоянием не убывает. Тем самым, при малых интенсивностях света континуальная модель оказывается непригодной.

Идею такого описания можно угадать, исследуя свойства света в рамках континуальной модели классической физики. В ней электромагнитное излучение представляют в виде совокупности независимых гармонических волн или нормальных мод с определенными значениями w и k. Проверкой того, что подобное описание адекватно физическому объекту, является тот факт, что для электромагнитных волн любого частотного диапазона наблюдаются явления интерференции и дифракции.

Возникает вопрос, наблюдаются ли подобные явления в случае света малой интенсивности, т.е. для небольшого числа одинаковых фотонов. Опыты по пропусканию фотонов вдоль оси достаточно узкой щели показывают, что после щели они регистрируются в пределах области, превышающей размер щели, хотя это не укладывается в рамки корпускулярной модели. Более того, совокупность последовательно зарегистрированных фотонов полностью воспроизводит картину, соответствующую дифракции электромагнитного излучения с частотой w и волновым числом k, несмотря на то, что каждый фотон регистрируется только один раз и притом локально, т.е. в одной точке пространства. Из этого можно сделать как минимум три важных заключения.

Во-первых, локальность регистрации свидетельствует о том, что к фотону в момент регистрации все-таки можно применить модель частицы. Во-вторых, наблюдаемый эффект колоколообразного распределения числа попаданий одинаковых фотонов в разные участки щели следует приписать неконтролируемому воздействию щели на каждый фотон, которое и вызывает изменение его первоначального состояния. В-третьих, признаками волны, т.е. способностью к дифракции, следует наделить состояние фотона до щели. Дополнительным опытом (подставляя аналогичную щель на пути фотона, испытавшего уже дифракцию на первой щели) можно убедиться, что состояние фотона (если он не был зарегистрирован) не потеряло этого свойства и за щелью. Отсюда и возникает идея описывать состояние фотона до щели бегущей гармонической волной типа . Однако эту волну, по форме напоминающую поведение электрического поля в распространяющейся электромагнитной волне большой интенсивности, в данном случае не следует связывать c электрическим или магнитным полями.

Таким образом, фотон – это материальный объект микромира. Если исходить из идеи единства природы, то аналогичное описание должно быть эффективно и в отношении любых других микрообъектов – электронов, протонов, нейтронов и т.п. Каждому из них, помимо известных из классической физики характеристик – энергии e, импульса р, момента s – необходимо сопоставить и характеристики другого типа, имеющие смысл характеристик его состояния, которые учитывают наличие неконтролируемого воздействия макроскопического окружения. Для свободной микрочастицы с ненулевой массой такими характеристиками являются частота , волновое число (или длина волны де Бройля) lБр и спиновые квантовые числа.

Само микросостояние напоминает гармоническую бегущую волну и описывается волновой функцией или волной де Бройля. При прохождении пучка электронов с одинаковой энергией и импульсом, как и в случае пучка фотонов, наблюдается явление дифракции, хотя каждый электрон регистрируется только в одной точке пространства, то есть локально. Вследствие этого состояние микрочастицы задается амплитудой вероятности обнаружения электрона в данном месте в данный момент времени, то есть отвечает описанию события в неклассической физике.

Если микрочастица вынуждена совершать ограниченное движение (как электрон в кристалле или в атоме, атом в молекуле и т.п.), то ее состояние напоминает стоячую волну, представляющую собой суперпозицию двух бегущих в разные стороны волн одинаковой частоты. Длины волн и волновые числа стоячих волн, описывающих микросостояния, зависят от дискретных индексов, которые в этом случай принято называть квантовыми числами. В результате физические характеристики микрообъекта, выраженные через характеристики состояния, также оказываются дискретными, или квантованными. К ним относятся, как правило, энергия, а также импульс или момент. Тем самым, наблюдаемая на опыте дискретность значений физических величин, которые в классической физике были непрерывными, возникает неслучайно. Она отражает фундаментальную роль другой стороны физической реальности – состояния микрообъекта. Квантовые числа – это как раз те самые характеристики состояния, от которых в данных задачах зависят фундаментальные характеристики микрообъектов.