Концепция макросостояний объектов

Тепловое равновесие как макросостояние.

Как следует из сказанного выше, для микромира типична повышенная чувствительность микросостояний к внешним квантоводинамическим воздействиям. Как правило, такие воздействия оказываются неконтролируемыми, в связи с чем в микромире приходится пользоваться менее жестким, чем в классической физике описанием – вероятностным.

Если теперь обратиться к макрообъектам, то, казалось бы, ничего подобного с ними происходить не может. Любой макрообъект содержит огромное число атомов (порядка числа Авогадро N@6×1026 атомов в киломоле), совершающих беспорядочное движение. Масса его тем самым велика. На первый взгляд, контакт с другим подобным макрообъектом должен был бы гасить любые неконтролируемые воздействия. Более того, можно ожидать, что описание макрообъекта в целом не должно существенно зависеть от свойств отдельного атома, а потому быть проще и грубее. Однако в действительности оправдывается лишь последнее предположение, а неконтролируемое воздействие окружения, и называемое тепловым для макрообъектов также оказывается существенным фактором, приводящим, как и в случае микрообъектов, к флуктуациям их характеристик. Об этом подробнее будет сказано позже.

Прежде всего отметим важный опытный факт: любая макросистема, находящаяся в фиксированных внешних условиях, независимо от ее начальных свойств с течением времени самопроизвольно переходит в состояние, называемое тепловым равновесием. В этом состоянии она может находиться сколь угодно долго, пока не изменятся внешние условия. Состояние теплового равновесия принято называть термодинамическим состоянием или, короче, – макросостоянием.

Что касается макрообъекта, то его макросостояние задается совокупностью макропараметров. Некоторые из них относятся к характеристикам макрообъекта самого по себе. Это внутренняя энергия, число частиц, объем и т.п. Другие относятся к термостату. Это температура, давление и химический потенциал. В условиях теплового равновесия предполагается, что эти характеристики внешнего неконтролируемого воздействия можно приближенно сопоставить и самому исследуемому макрообъекту. Однако точность этого сопоставления зависит от соотношения числа частиц в макрообъекте и термостате. Если в предельном случае макрообъект содержит достаточно малое число частиц, то флуктуации макропараметров могут быть весьма значительными.

Детерминированное и стохастическое движения. Ограничение воздействия на макроуровне как фундаментальный закон природы.

В случае микрообъектов мы имели дело со слабым неконтролируемым квантовым воздействием, определяемым постоянной. Планка. Это воздействие оказывается существенным в силу того, что сами объекты, на которое оно производится, малы. Иными словами, их микросостояния чувствительны к столь слабому воздействию.

До последнего времени представление о наличии неконтролируемого теплового воздействия не было общепринятым. Более того, традиционно считалось, что допущение его – это дань нашему неумению описать сколько-нибудь подробно поведение отдельных микрочастиц, образующих макрообъекты. Поскольку общее число таких микрочастиц (например, атомов) порядка числа Авогадро NA, возможность их последовательного описания обычно связывалось с прогрессом вычислительной техники. На самом деле, фундаментальный факт наличия теплового равновесия, обладающего упомянутыми выше свойствами, показывает, что характеристики макрообъектов вообще не зависят от деталей поведения составляющих их микрочастиц. Одновременно анализ броуновского движения показывает неустранимость теплового воздействия на любые макрообъекты.

В связи с этим возникает вопрос о месте человека как исследователя и интерпретатора природы в макромире и его роли в системе «объект плюс окружение». В микромире человек вместе со своими приборами, будучи – макрообъектом, безусловно встроен в макроокружение микрообъектов и поэтому сам оказывает на них неконтролируемое квантовое воздействие. В свою очередь, в макромире человек со своими приборами вынужден встраиваться в макрообъекты, чтобы вместе с ними воспринимать неконтролируемое тепловое воздействие термостата. По этой причине между приборами (т.е. человеком) и макрообъектами также должны реализовываться условия теплового равновесия, чтобы совместно воспринимать воздействие термостата. Что касается термостата, то это по существу мегаобъект, ибо всегда предполагается, что для частиц в макрообъекте и термостате справедливо неравенство N объект << N термостат.

Таким образом, хотя описание природы на микроуровне и на макроуровне кардинально отличаются друг от друга, с точки зрения стратегии познания различие между ними не так велико. Фактически в нашем случае речь идет о наличии ограничения на минимальное воздействие со стороны внешнего окружения и выбора человеком позиции наблюдения, адекватной условиям эксперимента.

Возникает вопрос, какие же новые качества приобретают макросистемы при приближении к тепловому равновесию. В классической стратегии познания понятие теплового равновесия отсутствует, ибо в ней все частицы макросистемы совершают строго детерминированное движение по своим траекториям. Такому детерминированному движению обычно принято противопоставлять хаотическое движение.

Однако природа хаоса бывает различной. Очень часто хаотичность движения возникает вследствие неточности задания начальных данных или условий контролируемого внешнего воздействия. Вместе с тем, если эти неточности в начальный момент времени известны точно, то движение все равно будет предсказуемым, а потому – детерминированным, но только соответствующие предсказания будут справедливы не для одной частицы, а для совокупности частиц. При этом никакого теплового равновесия не возникает.

Макропараметры как характеристики объектов и их макросостояний в тепловом равновесии.

Макропараметры – это характеристики объектов и их макросостояний в условиях теплового равновесия. Они отличаются тем, что могут быть измерены макроскопическими: приборами стой или иной степенью точности. Эти приборы являются достаточно «грубыми», так что их показания не зависят от поведения отдельных микрочастиц макрообъекта.

К числу часто используемых макропараметров относится объем V и масса М макрообъекта, число N микрочастиц в нем, внутренняя энергия е и т.п. Все эти макропараметры являются экстенсивными. Их можно отнести как к объекту в целом, так и к его малым частям, причем для подобных характеристик выполняется требование аддитивности: А=åAi. Иначе говоря, это характеристики, в равной мере имеющие смысл как для микро-, так и для макрообъектов.

В то же время в тепловом равновесии на опыте встречаются макропараметры иного рода. Их называют интенсивными, и они отличаются тем, что могут быть применены только к макрообъекту в целом, т.е. обладают свойством A=A1=.=Аn. Это в свою очередь означает, что подобные величины – это специфические характеристики макросостояния, в котором находится макрообъект. Они отражают условие теплового равновесия объекта и термостата и поэтому не зависят от конкретных свойств макрообъекта, т.е. являются универсальными. Среди таких макропараметров важнейшим является температура.

Интенсивные макропараметры играют существенную роль при определении условий теплового равновесия. Это равновесие устанавливается между рассматриваемым макрообъектом и термостатом в результате тех или иных контактов через разграничивающую их поверхность: Все эти контакты в конце концов можно свести к трем основным типам.

Между макрообъектом и термостатом, может иметь место механический (силовой) контакт, связанный с тем, что над макрообъектом совершается работа с помощью макроскопических сил. Простейшим проявлением его может служить работа при расширении или сжатии газа. Условием равновесия при механическом контакте служит равенство давлений: P1 = Р2.

Между макрообъектом и термостатом может установиться тепловой (энергетический) контакт, связанный с тем, что происходит обмен энергией на граничной поверхности за счет беспорядочных ударов молекул. В отличие от механического контакта изменение энергии происходит здесь на микроуровне без изменения объема макрообъекта, изменения массы вещества в целом и т.п. Установление равновесия при тепловом контакте отвечает равенству потоков энергии через граничную поверхность, а признаком установления равновесия является равенство температур: Т1=Т2. Фактически этим условием пользуются и для измерения температуры, считая, что в условиях теплового равновесия в системе из трех объектов: исследуемого макрообъекта, специального макрообъекта, называемого термометром, и термостата выполняется равенство:

Т объект = Т прибор = Т термостат.

Перечислим важнейшим свойства температуры как характеристики макросостояния в тепловом равновесии, следующие из многочисленных опытов:

1. Понятие температуры имеет смысл для макрообъектов и к отдельным микрочастицам непосредственно оно не применимо.

2. Оно имеет четкий смысл только в тепловом равновесии и вблизи него.

3. В тепловом равновесии макрообъекты различной физической природы, погруженные в один и тот же термостат, имеют одинаковую температуру.

4. Если Т1 ¹ Т2, то соответствующие макрообъекты не находятся в тепловом равновесии. При Т1 > Т2 имеет место поток энергии от объекта А1 к объекту А2.

5. Все термометры измеряют одну и ту же характеристику, которую можно назвать температурой термостата. Тем самым температура – это макропараметр, отражающий наличие неконтролируемого теплового воздействия на макрообъект.

Наконец, возможно установление равновесия и при корпускулярном (диффузионном) контакте, когда макрообъект и термостат обмениваются отдельными микрочастицами. Подобный контакт происходит, в частности, между жидкой водой и водяным паром в условиях равновесия, в замкнутом сосуде. В этом случае одновременно идут процессы парообразования и конденсации, причем в тепловом равновесии происходит непрерывный обмен молекулами между жидкостью и паром. Условие равновесия при корпускулярном контакте имеет вид: m1 = m2, где величина m называется химическим потенциалом, который характеризует энергию, переносимую одной микрочастицей через границу между двумя макрообъектами при тепловом равновесии.

Как следует из опыта при тепловом равновесии между макропараметрами – характеристиками макрообъекта и его макросостояния – устанавливаются устойчивые взаимосвязи. Они описываются уравнениями состояния. Простейшим пример – уравнение Клапейрона-Менделеева для давления Р одного моля идеального газа P=RT/V, где R – универсальная газовая постоянная, V – объем сосуда, Т – температура, которую принято называть абсолютной и отсчитывать от Т= 0. Знакомая в повседневной жизни температура q по шкале Цельсия выражается через абсолютную температуру Т формулой: q=Т-273,15, т.е. отличается от абсолютной температуры только выбором начала отсчета.

Уравнения состояния для макрообъекта имеют смысл не только в фиксированный момент времени. Если изменения внешних условий, характеризующих контакт макрообъекта с термостатом, происходят медленно и обратимо, то соответствующие уравнения состояния справедливы в любой момент времени. Такие изменения называются равновесными макропроцессами. В этом случае макропараметры меняются синхронно, не нарушая условия теплового равновесия. Если же эти условия не выполнены, макропроцессы являются неравновесными и необратимыми.

Разумеется, при любом макропроцессе должен выполняться фундаментальный закон сохранения энергии изолированной макросистемы. Если исключить поступательное и вращательное движения объекта как целого, выбрав подходящую систему отсчета, то энергия изолированной системы сводится только к его внутренней энергии:

(3.8).

B случае, когда макрообъект взаимодействует с термостатом, полную энергию этих двух макрообъектов, образующих изолированную макросистему, можно представить в виде суммы энергий составляющих ее макрообъектов:

(3.9),

поскольку малой энергией взаимодействия двух макрообъектов можно пренебречь: евз<<еi. В результате закон сохранения энергии для изолированной макросистемы, состоящей из макрообъекта и термостата, в ходе равновесного макропроцесса принимает вид

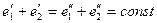(3.10),

где – внутренние энергии в начале макропроцесса, а – те же величины в конце его.

Отсюда следует, что передаваемая в ходе макропроцесса доля энергии равна

(3.11),.

Она определяется типом контакта макрообъекта и термостата.

Конечно, свойства термостата нам неизвестны, так что представляет интерес выяснение физического смысла как самой внутренней энергии е макрообъекта, так и ее изменения Dе в ходе равновесных макропроцессов. Например, для газа в сосуде объемом V при тепловом контакте энергия имеет вид соотношения е=е (V,T), которое также имеет смысл уравнения состояния газа, в частности, для одного моля газа из атомов при высоких температурах

(3.12).

Указанное обстоятельство, как показывает опыт, непременно сказывается на возможности дальнейшего использования энергии макрообъекта. Качественную (упорядоченную) энергию можно полностью потратить на совершение какой-либо работы над термостатом или полностью передать термостату в форме теплоты. При этом распределение микрочастиц самого макрообъекта по группам с определенной средней энергией не изменится. Некачественную (беспорядочную) энергию невозможно полностью потратить на совершение работы над термостатом без того, чтобы часть энергии в форме теплоты перешла бы термостату. Это можно сделать лишь частично.

Фактически подобное ограничение на изменение энергии макрообъекта в равновесных макропроцессах показывает, что в данном случае помимо закона сохранения энергии действует еще какой-то закон сохранения. Эта ситуация аналогична той, что имеет место при упругом столкновении двух частиц в динамике, когда передача кинетической энергии от одной частицы к другой полностью невозможна, поскольку одновременно справедливы два закона сохранения – энергии и импульса.

Величиной, сохраняющейся наряду с энергией в равновесных макропроцессах, является энтропия. Как уже отмечалось выше, она является мерой неупорядоченности макрообъекта. Через ее изменение DS теплота dQ записывается в виде dQ=TDS, так что теплота dQ имеет смысл изменения внутренней энергии Dе макрообъекта при фиксированной температуре за счет изменения энтропии DS, т.е. за счет изменения степени упорядоченности движения микрочастиц в макрообъекте.

Энтропия S является важнейшим макропараметром, характеризующим макросостояние и не имеющая аналогов в механике. Для идеального газа энтропия S = S(V,T) зависит от объема V и абсолютной температуры Т, причем при Т ® 0 энтропия S ® 0. Это означает, что вблизи абсолютного нуля температуры макрообъект становится полностью упорядоченным и теряет чувствительность к тепловому воздействию. Разумеется, он сохраняет чувствительность к квантовому воздействию, ибо фактически находится в определенном микросостоянии.

Как уже отмечалось выше, энтропия, а значит, и степень неупорядоченности изолированного макрообъекта, в ходе равновесных макропроцессов не меняется: DS равновес=0. В то же время для неравновесных макропроцессов в изолированном макрообъекте справедлив закон возрастания энтропии: DS неравновес>0: Если же макрообъект не изолирован, то в общем случае имеют место оба результата: возрастание энтропии внутри макрообъекта: DS внутр>0 и изменение энтропии макрообъекта за счет ее получения извне, причем в этом случае возможен как прирост энтропии, так и ее убыль: DS внеш>0 или DS внеш<0. Поэтому для неизолированных макрообъектов возможно в принципе как возрастание, так и убывание энтропии и даже ее сохранение:

DS = DS внут + DS внеш > 0, или = 0, или < 0. (3.13).

Тем самым, упорядоченность неизолированного макрообъекта в результате каких-либо макропроцессов может возрастать, убывать и в исключительных случаях сохраняться.

Два способа описания природы на макроуровне.

Найденное знаменитым американским ученым Гиббсом распределение микрочастиц по энергиям универсально, т.е. не зависит ни от выбора макрообъекта, ни от типа входящих в него микрообъектов, и определяется только особенностями контакта макрообъекта с термостатом. По этой причине соответствующее микросостояние обязательно зависит от абсолютной температуры термостата Т, а в более общих случаях от химического потенциала m и давления Р.

Тем самым макропараметры Т, m, Р, характеризующие макросостояние макрообъекта, входят в качестве фиксированных характеристик в описание микросостояния составляющих его микрообъектов. Они никак не связаны с характеристиками микрообъектов и поэтому не могут быть выражены через эти характеристики. В то же время макропараметры, являющиеся характеристиками макрообъектов самих по себе и имеющие аналоги на микроуровне (энергия, число частиц и т.п.), могут быть вычислены по известному микросостоянию в тепловом равновесии. В этом случае соответствующие макропараметры оказываются средними значениями микропараметров по совокупности микрочастиц, составляющих макрообъект, в частности, внутренняя энергия макрообъекта имеет вид

(3.14),

где – характерные энергии микрочастиц, a WG – распределение Гиббса, имеющее смысл вероятности того, что микрочастица входит в состав групп с энергией в условиях теплового равновесия, характеризуемого температурой термостата Т.

Особо следует сказать о самом распределении Гиббса и о его связи с таким фундаментальным макропараметром, как энтропия.

Энтропия может быть вычислена путем усреднения самого распределения Гиббса. После такого усреднения всякая зависимость от характеристик микрочастиц в энтропии исчезает, и она оказывается зависящей от макропараметров, включая макропараметры Т и m, никак не связанные с характеристиками микрочастиц. Можно сказать, что фактически энтропия является макроскопическим «образом» распределения Гиббса. Она является макропараметром, воплощающим в себе существенные черты микросостояния совокупности микрочастиц, образующих макрообъект.

Таким образом, из изложенного следует, что в принципе возможны два независимых способа описания природы на макроуровне. В одном из способов описания используются макропараметры, характеризующие макрообъект и его макросостояние в условиях теплового равновесия. Все они равноправны и взаимосвязи между ними определяются уравнением состояния. Изменение энергии макрообъекта в равновесном макропроцессе определяются формулой

(3.15),

называемым основным термодинамическим равенством. При этом энтропия S характеризует степень неупорядоченности макрообъекта.

В другом способе описания исходят из универсального микросостояния в тепловом равновесии, называемого распределением Гиббса. Оно зависит от макропараметров, которые в первом способе фиксировали макросостояние и поэтому они не могут быть вычислены по распределению Гиббса. В же время макропараметры, относящиеся к макрообъекту, например, энергию e можно вычислить как некие средние значения по распределению Гиббса. При этом то же самое изменение энергии макрообъекта в равновесном макропроцессе, что и выше можно записать в виде

(3.16),

где первый член соответствует передаче теплоты Q, а второй член – работе (-dA).