Флуктуации и альтернативная корреляция между ними в микромире

Подчеркнем еще раз, что необходимо отличать понятие флуктуации от понятия дисперсии как их математической меры подобного отклонения. В связи с этим применение теории вероятности в качестве вспомогательного средства анализа природных явлений в условиях неполноты информации или ошибок экспериментатора в принципе допустимо и в классической физике. Тем самым в ней возможно использование дисперсий физических характеристик при анализе конкретных условий и результатов эксперимента.

Однако в классической физике подобные дисперсии характеризуют только экспериментальные или теоретические неточности этих величин, а вовсе не флуктуации соответствующих характеристик. Это обстоятельство находит отражение в том, что в классической стратегии мышления предполагается возможность независимого обращения любой из этих дисперсий в нуль в случае повышения качества проведения эксперимента или устранения иных источников ошибок. Разумеется, наличие каких-либо корреляции между дисперсиями разных физических характеристик в классической физике не предполагается, что лишний раз подтверждает аппаратурный и тем самым субъективный характер соответствующих неточностей.

Наоборот, в неклассической физике флуктуации физических характеристик являются органичной частью описания природы, будучи существенно связаны с наличием неконтролируемого воздействия того или иного типа. Последнее находит отражение в существовании нетривиальных корреляций между флуктуациями важнейших физических характеристик, относящихся к объекту самому по себе и к его состоянию. В последнем находит свое отражение идея целостности природы в неклассической стратегии мышления.

Впервые на существование нетривиальных флуктуации физических характеристик в микромире и корреляции между ними указал Гейзенберг в 1927 году. Анализируя многочисленные эксперименты, он установил, что для микрочастицы в определенной макрообстановке справедливы следующие соотношения между флуктуациями ее импульса и координаты

(11.1).

Здесь Dр_х и Dх – дисперсии импульса р_х = mv_x и координаты х микрочастицы соответственно, a 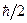– мера корреляции между ними, вызванной наличием неконтролируемого квантового воздействия.

Это соотношение, называемое соотношением неопределенностей (СН) Гейзенберга, демонстрирует наличие существенной корреляции между флуктуациями импульса и координаты микрочастицы, движущейся вдоль одной и той же оси. Вместе с тем эта корреляция отражает наличие неконтролируемого квантового воздействия и носит своеобразный альтернативный характер. Фактически эта корреляция демонстрирует согласованное поведение флуктуации как бы в противофазе друг с другом, когда дисперсии Dр и Dх обратно пропорциональны друг другу. Из этого обстоятельства прежде всего следует, что в природе не существуют такие микросостояния, в которых для микрочастицы одновременно было бы Dр_х=0 и Dх=0. Если же одна из дисперсий в данном микросостоянии обратилась бы в нуль, то другая дисперсия, согласно СН Гейзенберга должна была бы стремиться к бесконечности. Отсюда следует, что в природе не реализуются микросостояния, в которых импульс частицы и ее координата одновременно могли бы принимать точные значения.

Иногда подобную ситуацию называют корпускулярно-волновым дуализмом, подразумевая тем самым, что микрочастицы якобы воплощают в себе характерные черты сразу двух фундаментальных классических моделей объектов – корпускулы и континуума (волны). Разумеется, представить это наглядно невозможно, да и не нужно. На самом деле в каждом случае одна из двух характеристик: либо х, либо р_x относится к самому микрообъекту, а другая – к его микросостоянию, формируемому неконтролируемым квантовым воздействием макроокружения. При этом микросостояния, в которых микрочастица обладает либо точным значением импульса, либо точным значением координаты также являются идеализированными. Фактически на опыте мы всегда имеем дело с микросостояниями, в которых одновременно флуктуируют и импульс и координата, но при этом их флуктуации коррелированы между собой, согласно СН Гейзенберга. Как показал последующий анализ, корреляции, аналогичные СН Гейзенберга, имеют место в микромире для различных микрообъектов и их различных характеристик, а не только для координаты и импульса одной микрочастицы.