Определение ошибок выборки

Разность между соответствующими показателями выборочной и генеральной совокупностей называется ошибкой выборки.

- генеральное среднее;

- выборочное среднее;

- генеральная дисперсия;

- выборочная дисперсия;

Ошибки выборки подразделяют на ошибки регистрации и ошибки репрезентативности.

Ошибки регистрации возникают из-за неправильных или неточных сведений. Источником таких ошибок могут быть: непонимание вопроса, невнимательность регистратора, пропуск или повторный счет некоторых единиц совокупности.

Среди ошибок регистрации выделяют систематические, т.е. обусловленные причинами, действующими в каком-то одном направлении и искажающие результаты работы (округление цифр, тяготение к полным десяткам и сотням и т.д.), и случайные, проявляющиеся в различных направлениях, уравновешивающие друг друга и лишь изредка дающие заметный суммарный итог.

Ошибки репрезентативности также могут быть систематическими и случайными.

Изучение и измерение случайных ошибок репрезентативности является основной задачей выборочного метода.

При случайном и механическом отборах средняя ошибка выборки для средней величины определяется по формуле:

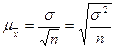- при повторном отборе;

- при бесповторном отборе,

- объем выборки,

- объем генеральной совокупности.

На практике значение генеральных параметров, как правило, не известно. Поэтому их заменяют исправленными выборочными характеристиками:

При

Формулы для расчета средней ошибки выборочной доли имеют следующий вид:

- при повторном отборе;

- при бесповторном отборе;

- дисперсия доли; 0.25=0.5(1-0.5)

Это так называемые средние или стандартные ошибки.

Предельная ошибка выборки представляет собой t-кратную среднюю ошибку.

,

Здесь t – коэффициент доверия, который определяется по таблице значений интегральной функции Лапласа при заданной доверительной вероятности (для больших выборок , n>30).

	0,683	0,954	0,997
t

Зная предельную ошибку, можно определить доверительные интервалы, в которых находятся значения генеральных параметров.

Пример:

Для определения среднего срока пользования краткосрочным кредитом в банке была произведена 5% механическая выборка, в которую попали 200 счетов. По результатам выборки установлено, что средний срок пользования кредитом составляет 60 дней при среднеквадратичном отклонении 20 дней.

В 8 счетах срок пользования кредитом превышал 6 месяцев. Необходимо с вероятностью 0,99 определить пределы, в которых находится срок пользования краткосрочным кредитом банка и доля краткосрочных кредитов со сроком пользования более полугода.

Решение:

Среднюю ошибку выборки определим по формуле для бесповторного отбора.

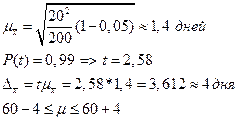(по таблице)

Т.е. с вероятностью 0,99 можно утверждать, что средний срок пользования краткосрочным кредитом составляет от 56 до 64 дней.

По итогам выборки определим долю кредитов со сроком пользования более полугода.

С вероятностью 0,99 можно гарантировать, что доля кредитов банка со сроком использования более полугода оставляет общего числа кредитов.