
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Определение оптимальной численности выборки
На практике обычно расчет объема выборки производят по формуле для повторного отбора:
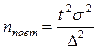
Если полученный объем выборки превышает 5% численности генеральной совокупности, то расчеты корректируют на бесповторность:

В данных формулах присутствуют значения генеральной дисперсии, которые, как правило, неизвестны. Для ее оценки можно использовать:
1. Выборочную дисперсию по данным прошлых или пробных обследований.
2. Дисперсию, найденную из соотношения для среднего квадратичного отклонения:
 (если все х >0 и х min à 0)
(если все х >0 и х min à 0)
3. Дисперсию, вычисленную из соотношения для нормального распределения

4. Дисперсию, определенную из соотношения для асимметричного распределения

В качестве оценки генеральной дисперсии доли используют максимально возможную дисперсию альтернативного признака:

Пример: Определить численность выборки по следующим данным. Для определения средней цены огурцов на 5000 рынках города предполагается провести выборочную регистрацию цен. Известно, что цены за 1 кг. огурцов колеблются от 40 до 70 руб/кг. Сколько торговых точек необходимо обследовать, чтобы с вероятностью 0,954 ошибка выборки при определении средней цены не превышала 2 руб. за 1 кг.
Решение: Предположим, что распределение цен соответствует нормальному закону. Тогда

P(t) = 0,954. Следовательно t = 2.


Поскольку доля отбора не превышает 5%, то к формуле бесповторного отбора можно не переходить. Т.е. для того, чтобы с вероятностью 0,954 гарантировать, что ошибка при определении цены на огурцы не превысит 2 руб./кг. необходимо исследовать 25 торговых точек на рынках города.
Определение: Относительная ошибка выборки – это отношение предельной ошибки выборки к среднему значению признака, выраженное в %.

Расчёт объема выборки при заданном уровне относительной ошибки выборки осуществляется по формулам:


 - коэффициент вариации
- коэффициент вариации
Пример: В городе зарегистрировано 30000 безработных. Для определения средней продолжительности безработицы организуется выборочное обследование. По данным прошлых лет известно, что коэффициент вариации продолжительности безработицы составляет 40%. Какое число безработных необходимо охватить выборочным наблюдением, чтобы с вероятностью 0,997 утверждать, что полученная предельная ошибка выборки не превышает 5% средней продолжительности безработицы.
Решение: P(t) = 0,997. Следовательно, t = 3.

Объем выборки всегда округляют в большую сторону.
Ответ: 566.
Дата добавления: 2014-12-23; просмотров: 392; Мы поможем в написании вашей работы!; Нарушение авторских прав |