Частная корреляция

Если имеются 3 признака XYZ и известны коэффициенты корреляции между ними, то можно определить частные коэффициенты корреляции, которые показывают тесноту корреляционной связи между двумя из этих величин, при условии, что третья величина постоянная, т.е. влияние этой величины на корреляцию между двумя другими исключено.

Пример: Частный коэффициент корреляции между двумя коэффициентами Y и X при постоянном признаке Z:

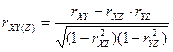
Временные ряды

Временной (динамический ряд) – последовательность значений некоторого статистического показателя в определенные интервалы (или моменты) времени.

Значения показателя – уровни ряда.

Уровни динамического ряда могут быть абсолютными, средними или относительными величинами.

Временные ряды делятся на интервальные и моментные.

В интервальном ряду приводятся данные, характеризующие величину показателя за определенный период.

Пример: Объем продаж телевизоров LG в магазине Элекам по месяцам:

В моментном ряду динамики приводятся данные характеризующие явления на определенные моменты времени или дату. Уровни моментных динамических рядов суммировать нельзя.

Пример моментного ряда – величина суммы вклада на 1 число каждого месяца.

При формировании рядов динамики следует соблюдать сопоставимость уровней, образующих ряд (одинаковая методология их исчисления), одинаковая полнота охвата различных частей явления представляемого рядом динамики.

Для моментных рядов характерна неизменность даты учета (количество товара на складе на первое число месяца)