
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Целью регрессионного анализа в случае парной регрессии является предсказание значения результативного признака Y при определенном значении факторного признака X

В случае множественной корреляции исследуется зависимость отклика системы от нескольких факторов

Изучение множественной корреляции начинается с анализа матрицы парных коэффициентов корреляции, что позволяет произвести отбор факторов, включаемых в модель множественной зависимости
| Признак | y | x1 | x2 | … | xk |
| y | ry,x1 | ry,x2 | … | ry,xk | |
| x1 | rx1,y | rx1,x2 | … | rx1,xk | |
| x2 | rx2,y | rx2,x1 | … | rx2,xk | |
| … | … | … | … | … | … |
| xk | rxk,y | rxk,x1 | rxk,x2 | … |
При построении многофакторных моделей должно соблюдаться требование наименьшей коррелируемости включенных в модель признаков–факторов, т.е. отсутствия мультиколлинеарности.  . При невыполнении хотя бы одного неравенства следует исключить факторный признак с менее тесной связью с Y.
. При невыполнении хотя бы одного неравенства следует исключить факторный признак с менее тесной связью с Y.
Следует учитывать, что число факторов, включаемых в модель, должно быть в 5-6 раз меньше, чем число единиц, входящих в совокупность.
Совокупный коэффициент корреляции определяется следующим образом:

 - определитель матрицы парных коэффициентов корреляции,
- определитель матрицы парных коэффициентов корреляции,
 - определитель матрицы, получаемый из матрицы парных коэффициентов корреляции путем вычеркивания 1 строки и 1 столбца,
- определитель матрицы, получаемый из матрицы парных коэффициентов корреляции путем вычеркивания 1 строки и 1 столбца,
 - коэффициент детерминации. Он показывает, в какой мере вариация результативного признака обусловлена влиянием признаков-факторов, включенных в уравнение множественной регрессии. R не может быть меньше, чем любой из образующих его парных коэффициентов корреляции. Чем ближе R к 1, тем меньше роль неучтенных в модели факторов и тем более оснований считать, что параметры регрессионной модели верно отражают степень эффективности включенных в нее факторов.
- коэффициент детерминации. Он показывает, в какой мере вариация результативного признака обусловлена влиянием признаков-факторов, включенных в уравнение множественной регрессии. R не может быть меньше, чем любой из образующих его парных коэффициентов корреляции. Чем ближе R к 1, тем меньше роль неучтенных в модели факторов и тем более оснований считать, что параметры регрессионной модели верно отражают степень эффективности включенных в нее факторов.
Для сравнения роли различных факторов в формировании моделируемого показателя определяют α-коэффициенты (коэффициенты эластичности) и β-коэффициенты.
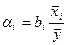 показывает, на сколько процентов в среднем изменяется результативный признак Y c изменением фактора Xi на 1%. bi – коэффициент регрессии при i-ом факторе.
показывает, на сколько процентов в среднем изменяется результативный признак Y c изменением фактора Xi на 1%. bi – коэффициент регрессии при i-ом факторе.
β-коэффициент показывает, на какую часть среднего квадратического отклонения изменится результативный признак при изменении соответствующего фактора Хi на величину его среднего квадратического отклонения:
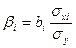
Рассмотрим простейшую модель линейной регрессии с 2-мя факторами X и Z
Y=b0+b1x+b2z

Дата добавления: 2014-12-23; просмотров: 260; Мы поможем в написании вашей работы!; Нарушение авторских прав |