
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Линии регрессии. Метод наименьших квадратов (МНК).
Линии регрессии - это линии, отражающие основную форму зависимости отклика Y от факторного признака X. Определение вида этих линий – основная задача регрессионного анализа.

МНК позволяет определить параметры линии регрессии 
Ломаная линия, соединяющая фактические данные на корреляционном поле, называется эмпирической регрессией.
Основное требование МНК: Сумма квадратов отклонений эмпирических значений отклика от теоретических должна быть минимальной.
 или
или 
Отклонение 

Рассмотрим простейший случай – линейную регрессию.

Определим с помощью МНК неизвестные параметры a и b:

Решаем эту систему нормальных уравнений методом Крамера:

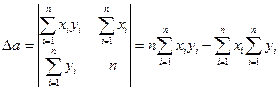
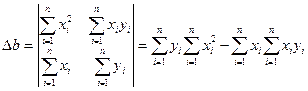
 (*)
(*)
Регрессия y на x задается следующей формулой : 


Это две различные прямые, пересекающиеся в точке  :
:

Одна из этих прямых y=ax+b получается в результате решения задачи минимизации суммы квадратов отклонений по вертикали, а другая (x=cy+d) - по горизонтали.
Для удобства определения параметров a и b можно использовать следующую таблицу:
| i | 
| 
| 
| 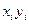
|
| … n | 
 …
…

| 
 …
…

| 
 …
…

| 
 …
…

|

| 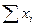
| 
| 
| 
|


Уравнение регрессии нужно в первую очередь для проведения прогноза (экстраполяции и интерполяции). При экстраполяции не рекомендуется выходить как в сторону больших, так и в сторону меньших значений по X за пределы, превышающие 1/3 размаха вариации по X.
Границы доверительного интервала определяются следующим образом:

 - значение точечного прогноза,
- значение точечного прогноза,
 -значение факторного признака, для которого выполняется прогноз,
-значение факторного признака, для которого выполняется прогноз,
m - число параметров в уравнении регрессии.
n-m - число степеней свободы,
a - уровень значимости, 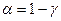 (в нашем случае a будет иметь смысл вероятности ошибки прогноза).
(в нашем случае a будет иметь смысл вероятности ошибки прогноза).
 - остаточное среднеквадратическое отклонение, скорректированное по числу степеней свободы.
- остаточное среднеквадратическое отклонение, скорректированное по числу степеней свободы.
Дата добавления: 2014-12-23; просмотров: 304; Мы поможем в написании вашей работы!; Нарушение авторских прав |