
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Смешанное соединение 1 страница
Схема упрощается путем замены параллельных и последовательных соединений сопротивлений на эквивалентные. Начиная с конца схемы сопротивления R2 и R3 включены параллельно, заменяем их на R23, а с R1 соединение последовательное.

Расчет ведется в обратном порядке:
1. По схеме 3находим I1 =U/R.
2. По схеме 2 находим U23 = I1R23.
3. По схеме 1 находим I2 = U23 /R2, I3 = U23 /R3.
4. Проверка: I1 = I2 + I3, U1I1 = I12R1 + I22R2 + I32R3 (баланс мощностей ).
Встречается также соединения в «треугольник» и в «звезду». Они взаимно преобразуются, и схема сводится к смешанному соединению с последовательным и параллельным соединением элементов.
Примеры решения задач
1.1.
 Дано: R1 = 4 Ом;
Дано: R1 = 4 Ом;
R2 = 6 Ом;
R3 = 10 Ом;
R4 = 15 Ом;
U = 120 В.
Определить: I, I1, I2, I3, I4, P.
Рис. 1.1
Упрощаем схему: R3 и R4 включены параллельно. Заменяем эквивалентным сопротивлением R34:

 Ом.
Ом.
Резисторы R2 и R34 включены последовательно. Заменяем их эквивалентным сопротивлением R234:

R234 = R2 + R34 ; R234 = 6 + 6 = 12 Ом.
Теперь имеем параллельное соединение, которое также приводим к одному эквивалентному сопротивлению R1234:

 ;
;  Ом.
Ом.
Расчет ведем в обратной последовательности:
1) по схеме 4 находим  ,
,  А.
А.
Мощность, отдаваемая генератором: Р = UI; Р = 120 · 40 = 4800 Вт;
2) по схеме 3 находим токи I1 и I2:
 ;
;  А;
А;
 ;
;  А;
А;
3) по схеме 2 находим напряжение U34:
U34 = I2 · R34; U34 = 10 · 6 = 60 В;
4) по схеме 1 определяем токи I3, I4:
 ;
; 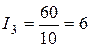 А;
А;
 ;
;  А;
А;
5) проверка: в узлах «а» и «в» проверяем первый закон Кирхгофа:
узел «а»: I = I1 + I2; 40 = 30 + 10;
узел «в»: I2 = I3 + I4; 10 = 6 + 4.
Первый закон Кирхгофа выполняется.
Составляем баланс мощностей (мощность, отдаваемая генератором, должна быть равна сумме мощностей всех потребителей):
Рген = ∑Рпотр;
UI = I12R1 + I22R2 + I32R3 + I42R4;
4800 = 302 · 4 + 102 · 6 + 62 · 10 + 42 · 15 = 4800.
Баланс мощностей соблюдается, значит задача решена верно.
1.2. Как изменятся показания приборов при замыкании выключателя SA?

Рис. 1.2
Р е ш е н и е. Замыкая выключатель, шунтируем сопротивление R. Сопротивление второй ветви уменьшается, следовательно, уменьшается сопротивление всей схемы Rсх. При неизменном напряжении сети ток I0 по закону Ома увеличится: 
Ток I1 не изменится, т.к. сопротивление R1 не меняется и напряжение не изменилось.
Ток I2 возрастает, что доказывается двумя способами:
по закону Ома  , где R = 0 при замыкании SA, и по первому закону Кирхгофа: I0 = I1 + I2, откуда I2 = I0 – I1.
, где R = 0 при замыкании SA, и по первому закону Кирхгофа: I0 = I1 + I2, откуда I2 = I0 – I1.
Напряжение на вольтметре pV2 возрастает до значения сетевого напряжения (ветви включены параллельно, а при разомкнутом SA напряжение U2 было меньше, т.к. U = U2 + UR (последовательное соединение R2 и R), а при замыкании SA показания вольтметра pV будут равны нулю.
1.3. Как изменятся показания приборов при замыкании выключателя SA?


Рис. 1.3
Р е ш е н и е. Имеем смешанное соединение. Ветви R1 и (R2 + R) соединены параллельно, а с резистором R0 последовательно. При замыкании выключателя резистор R шунтируется, сопротивление второй ветви уменьшается (R2 + R), проводимость ветви g2 возрастает. Первая и вторая ветви соединены параллельно, проводимость этого соединения (g12 = g1 + g2) также увеличивается, а сопротивление ветвей R12 уменьшается. Следовательно, уменьшается сопротивление всей схемы. По закону Ома общий ток I0 возрастает: 
Так как R0 и R12 соединены последовательно, напряжение сети делится: U = = U0 + U12, откуда U12 = U – U0 уменьшается (U0 = I0R0 увеличится). Ток  станет меньше. Изменение тока I2 по закону Ома не доказать:
станет меньше. Изменение тока I2 по закону Ома не доказать:  , т.к. уменьшились и напряжение ветви U12, и сопротивление ветви (R2 + R). Применяем первый закон Кирхгофа: I0 = I1 + I2, откуда I2 = I0 – I1. Ток I0 увеличился, а I1 уменьшился, следовательно, I2 возрастает. Показания вольтметра pV2 увеличатся по закону Ома: U2 = I2R2, а вольтметр pV покажет ноль.
, т.к. уменьшились и напряжение ветви U12, и сопротивление ветви (R2 + R). Применяем первый закон Кирхгофа: I0 = I1 + I2, откуда I2 = I0 – I1. Ток I0 увеличился, а I1 уменьшился, следовательно, I2 возрастает. Показания вольтметра pV2 увеличатся по закону Ома: U2 = I2R2, а вольтметр pV покажет ноль.
Глава 2. Расчет сложных цепей постоянного тока
Сложная цепь имеет два и более источника ЭДС, и направление токов нельзя определить без расчета.
Основные определения и законы Кирхгофа:
1. Ветвь – участок цепи с последовательным соединением элементов.
2. Узел – точка соединения нескольких ветвей.
3. Контур – любой замкнутый путь по цепи с началом и концом в одном узле.
4. Независимый контур – отличается от другого хотя бы одной ветвью.
| I закон Кирхгофа. | Алгебраическая сумма токов, сходящихся в узле, равна нулю, или сумма токов, подходящих к узлу, равна сумме токов, выходящих из узла: |

I1 + I2 – I3 + I4 – I5 = 0;
или
I1 + I2 + I4 = I3 + I5.
II закон Кирхгофа. В любом замкнутом контуре алгебраическая сумма ЭДС равна алгебраической сумме падений напряжений.
 .
.
Правило выбора знака: если ЭДС, ток совпадают с направлением обхода контура, берутся со знаком “плюс”, не совпадают – “минус”.
Методика расчета с использованием законов Кирхгофа
 1. Выбираем независимые контуры, например, I и II, произвольно задаемся направлением их обхода и направлением токов в ветвях (отмечено пунктиром).
1. Выбираем независимые контуры, например, I и II, произвольно задаемся направлением их обхода и направлением токов в ветвях (отмечено пунктиром).
2. Составляем (n – 1) уравнений по I закону, где n – число узлов, а недостающее число уравнений – по II закону.
3. Получаем систему уравнений:

Решаем, находим токи в ветвях. Если ток получился со знаком “минус”, значит он протекает в противоположном направлении.
4. Проверка правильности решения определяется соблюдением I закона Кирхгофа и баланса мощностей.
Необходимо иметь в виду, что источники ЭДС могут работать в режиме генератора (направления тока и ЭДС совпадают) и быть потребителем энергии, если такого совпадения нет.
Метод контурных токов

1. Определяемся с числом независимых контуров и считаем, что в каждом контуре проходит свой контурный ток. Произвольно задаемся их направлениями и направлением обхода контуров (берем все по часовой стрелке).
2. Составляем уравнения по II закону Кирхгофа для выбранных контуров с учетом того, что по некоторым ветвям проходят токи нескольких контуров, а для каждого контура имеем последовательное соединение элементов.
Имеем:
E1 – E2 = II (R1+R2) – IIIR2;
E2 – E3 = III (R2+R3) – IIR2.
3. Решаем систему уравнений, определяем контурные токи. Если ток получился со знаком “минус”, значит фактически он имеет противоположное направление.
Токи в ветвях определяем по соотношениям:
I1 = II; I3 = III; I2 = II-III
4. Проверка: I-й закон Кирхгофа и баланс мощностей.
Метод узлового напряжения (двух узлов)
Если электрическая цепь состоит только из параллельных ветвей, т.е. имеет всего два узла, напряжение между которыми называется узловым (Uaв), то его можно определить в общем случае по формуле:

 ,
,
где Ei – ЭДС; gi = 1/Ri – проводимость ветви.
ЭДС ветви берется со знаком “плюс”, если направлено к узлу, обозначенному первым индексом (а), и со знаком “минус”, если направлено ко второму узлу.
В нашем случае имеем:
 .
.
Зная узловое напряжение, можно каждую ветвь рассматривать в отдельности и определить токи.

Для пассивной ветви (где нет источника ЭДС) направление тока совпадает с направлением узлового напряжения, а для активных ветвей задаемся произвольно направлениями токов и составляем уравнения по II закону Кирхгофа:
-E1 = Uaв + I1R1; E2 = Uaв + I2R2; -E3 = Uaв + I3R3,
откуда определяем токи:
I1 = (-Uaв – E1)g1; I2 = (E2 - Uaв)g2; I3 = (–E3 - Uaв)g3.
Кроме рассмотренных применяются и другие методы расчета сложных цепей.
Примеры решения задач
2.1. В цепи ЭДС источников питания равны Е1, Е2, Е3, а сопротивления ветвей – соответственно r1, r2, r3, r4 (включая внутренние сопротивления источников питания). Определитеь силы токов во всех ветвях цепи и режим работы каждого из источников. Составьте баланс мощностей. Задачу решите двумя методами: узлового напряжения и контурных токов.
| Вариант | Данные к задаче № 1 | ||||||
| Е1, В | Е2, В | Е3, В | r1, Ом | r2, Ом | r3, Ом | r4, Ом | |
Р е ш е н и е. Определяем силы токов во всех ветвях цепи методом двух узлов. Предварительно направим все токи из узла «а».

Рис. 2.1
Определим напряжение между узлами «ав»:
 , (1)
, (1)
где Ei – ЭДС;
gi = 1/Ri – проводимость ветви.

Определим токи в ветвях:




Если направления токов и ЭДС совпадают, то источник ЭДС работает в режиме генератора, если нет – потребителя. Так как все токи совпадают с ЭДС, то все источники ЭДС работают в режиме генератора.
Составим баланс мощностей:
 ;
;
 ;
;
 кВт;
кВт;
 ;
;
 Вт.
Вт.
Баланс мощностей соблюдается.
Определим токи в ветвях методом контурных токов:

Выбираем контуры: I – r1E1E2r2; II – r2E2r4; III – r4E3r3.
Направления обхода и токов выбираем произвольно (по часовой стрелке). Составим уравнения по II закону Кирхгофа для каждого контура:




Применим правило Крамера:







Определим токи в ветвях:
I1 = II = 41,8 A;
I2 = III – II = 76,5 – 41,8 = 34,7 A;
I3 = IIII = 65,5 A;
I4 = III – IIII = 76,5 – 65,5 = 11 A.
Значения токов совпадают с предыдущим расчетом. Задача решена правильно.
Глава 3. Расчет нелинейных электрических цепей
К нелинейным электрическим цепям постоянного тока относятся электрические цепи, содержащие нелинейные сопротивления, обладающие нелинейными вольтамперными характеристиками (ВАХ) I(U), т.е. нелинейной зависимостью тока от приложенного к нелинейному сопротивлению напряжения.
Различают неуправляемые нелинейные сопротивления (лампы накаливания, газотроны, бареттеры, полупроводниковые диоды и т.д.), которые характеризуются одной вольтамперной характеристикой, и управляемые (многоэлектродные лампы, транзисторы, тиристоры и др.), которые характеризуются семейством вольтамперных характеристик.
Расчет нелинейных электрических цепей постоянного тока обычно осуществляют графоаналитическим методом. При этом можно использовать и аналитический метод расчета, который, однако, достаточно сложен. Для выполнения расчета нелинейных электрических цепей должна быть известна вольтамперная характеристика соответствующего нелинейного сопротивления, представленная в виде графика или таблицы.
При расчете электрических цепей с последовательным включением нелинейных (или линейных и нелинейных) сопротивлений R1 и R2 вольтамперные характеристики соответствующих сопротивлений I1(U) и I2(U) представляются в общей координатной системе. По ним строится общая вольтамперная характеристика I (U) всей нелинейной электрической цепи (рис. 3.1), абсцисса каждой из точек которой при заданном токе I (заданной ординате) находится как сумма соответствующих падений напряжения (U = U1 + U2) на этих сопротивлениях (R1 и R2), поскольку при последовательном соединении по сопротивлениям протекает один и тот же ток I цепи. Таким образом, по общей вольтамперной характеристике I(U) нелинейной цепи при заданном значении напряжения U и последовательном соединении сопротивлений легко определяют ток I в нелинейной цепи, а по заданному току I находят напряжение U, подводимое к нелинейной цепи, и напряжения U1 и U2 на каждом из последовательно соединенных сопротивлений.

Рис. 3.1
При параллельном соединении нелинейных (или линейных и нелинейных) сопротивлений R1 и R2 также строят общую вольтамперную характеристику I(U) нелинейной электрической цепи (рис. 3.2). При этом ординату каждой из точек общей вольтамперной характеристики при заданном подводимом к цепи напряжении U (заданной абсциссе) определяют как сумму токов в цепях соответствующих сопротивлений (I = I1 + I2), так как при параллельном соединении на всех сопротивлениях действует одно и то же напряжение U. Следовательно, при параллельном включении сопротивлений по общей вольтамперной характеристике I(U) и заданном значении напряжения U нетрудно определить и ток I в нелинейной электрической цепи. При заданном общем токе I также легко определить и напряжение U, подводимое к данной нелинейной электрической цепи, и токи I1 и I2, протекающие в цепи каждого из параллельно соединенных сопротивлений.

Рис. 3.2
Следует отметить, что изложенная методика расчета нелинейных электрических цепей при последовательном и параллельном соединении сопротивлений справедлива для любого числа сопротивлений, включенных в цепь последовательно или параллельно.
При расчете нелинейных электрических цепей со смешанным (последовательно-параллельным) соединением нелинейных (или линейных и нелинейных) сопротивлений (рис. 3.3) строят вольтамперную характеристику I(U1) параллельного участка цепи; при этом образуется нелинейная электрическая цепь с последовательным соединением сопротивлений, для которой строится общая вольтамперная характеристика I(U) с учетом того, что подводимое к цепи напряжение U при данном токе цепи I равно сумме напряжений на параллельном U1 и на последовательном U2 участках цепи (U = U1 + U2).

Рис. 3.3
Примеры решения задач
3.4. Нелинейные сопротивления R1 и R2, включенные последовательно в электрическую цепь постоянного тока (рис. 3.4а), имеют вольтамперные характеристики I и II, приведенные на рисунке 3.4б. Определите ток I в цепи и напряжения U1 и U2 на этих сопротивлениях, если приложенное к цепи напряжение U = 60 В. В каких пределах изменится напряжение ∆U цепи при изменении тока I от I1 = 25 мА до I2 = =175 мА?
Р е ш е н и е. Строят общую вольтамперную характеристику III указанных двух последовательно соединенных нелинейных элементов (рис.3.4б) исходя из условия, что подводимое к цепи напряжение U при данном токе I нагрузки равно сумме напряжений на сопротивлениях R1 и R2, т. е. U = U1 + U2.

а б
Рис. 3.4

а б
Рис. 3.5
Ток в цепи при напряжении U = 60 В согласно зависимости III определяется ординатой 0-5, соответствующей I2 = 175 мА.
Напряжение на участках цепи находят из графических зависимостей. При токе I2 = 175 мА U1 = 19 B (абсцисса 5-4), U2 = 41 В (абсцисса 5-3). При токе I1 = 25 мА напряжение, подводимое к цепи, U = 22 В. Следовательно, изменение подводимого к цепи напряжения при изменении тока в заданных пределах согласно рисунку 3.4б составляет: ∆U = 66 – 22 = 38 В.
3.5. В электрическую цепь постоянного тока (рис. 3.5а) при напряжении U = 30 В включены параллельно нелинейные сопротивления R1 и R2, вольтамперные характеристики I и II которых представлены на рисунке 3.5б. Определить общий ток I в цепи, токи I1 и I2 в ветвях.
Р е ш е н и е. Общая вольтамперная характеристика IV (рис. 3.5б) при параллельном соединении нелинейных сопротивлений построена сложением токов (ординат) зависимостей I и II при соответствующем напряжении. Ток нелинейного сопротивления R1 при заданном напряжении U = 30 В равен ординате 6-7: I1 = 205 мА. Ток нелинейного сопротивления R2 при том же напряжении U = 30 В равен ординате 6-8: I2 = 100 мА. Общий ток в неразветвленной части цепи равен ординате 6-9: I = I1 + I2 = 205 + 100 = 305 мА.
Глава 4. Резистивные нелинейные элементы
4.1. Выпрямители
Выпрямители предназначены для преобразования переменного напряжения в постоянное. В схему простейшего выпрямителя входят вентиль V, электрический фильтр Ф и сопротивление нагрузки Rн. B зависимости от числа рабочих полупериодов напряжения питания и различают одно- и двухполупериодные схемы выпрямления, а в зависимости от числа фаз – однофазные, трехфазные и многофазные.


Рис. 4.1
В качестве вентилей в выпрямителях обычно применяют кремниевые или германиевые полупроводниковые диоды. Они имеют несимметричную вольтамперную характеристику (ВАХ).
Идеализированная ВАХ и условное изображение вентиля показаны на рисунках.
4.2. Однополупериодное выпрямление
При положительном мгновенном значении напряжения, т.е. когда и > 0
(проводящее направление), сопротивление вентиля мало, а ток теоретически (согласно идеализированной ВАХ) бесконечно большой; при отрицательном напряжении, т.е. когда и < 0 (непроводящее направление), ток равен нулю.

Рис. 4.2
Схема замещения однополупериодного выпрямителя (без фильтра) с сопротивлением нагрузки Rн изображена на рисунке 4.3. Вентиль представлен в виде нелинейного сопротивления Rв, напряжение питания синусоидальное u= Uмsinωt.Вольтамперная характеристика цепи (кривая 3) построена в соответствии со вторым законом Кирхгофа, т.е. и = ив + ин, суммированием абсцисс ВАХ вентиля (кривая 1) и ВАХ линейного сопротивления нагрузки (прямая 2).

Рис. 4.3
Дата добавления: 2014-12-23; просмотров: 1558; Мы поможем в написании вашей работы!; Нарушение авторских прав |