
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Смешанное соединение 4 страница
Построим векторную диаграмму токов и треугольник мощностей, зная, что при подключении конденсатора активная мощность не изменится.
1. Определяем полную мощность, потребляемую катушкой:
S = UIк; S = 8 · 450 = 3600 BА.
2. Определяем угол φ:
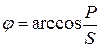 ,
, 
(cos φ = 0,55).
3. Определяем реактивную мощность, потребляемую катушкой:
Q = S · sinφ, Q = 3600 · sin 560 = 2980 ВАр.
При резонансе токов мы полностью компенсируем эту реактивную мощность и потребляемый из сети ток уменьшится, что видно на векторной диаграмме.
4. Рассчитываем емкость конденсатора:
 ;
;

5. Потребляемый ток будет:
I = Iк cosφ;
I = 8 · 0,55 = 4,4 А.
Ток снижается практически в 2 раза, но для этого требуется большая емкость конденсаторов, поэтому на практике не стремятся достигнуть cosφ = 1, а удовлетворяются меньшими значениями, порядка 0,9. Это определяется экономическим обоснованием.
5.8. Определите символическим методом результирующий ток в цепи и потребляемые мощности. Параметры схемы: U = 200 B, r1 = 2 Ом, r2 = 6 Ом, r3 = 16 Ом, xL = 8 Ом, хС = 12 Ом.

Р е ш е н и е. Изображаем сопротивление в комплексном виде и упрощаем схему так же, как делали на постоянном токе для смешанного соединения, заменяя параллельное соединение одним сопротивлением, а затем последовательное соединение тоже общим сопротивлением.

Имеем в общем виде:
 ;
;
 ;
;
 ;
;
 ;
;
 .
.
1. Решаем в числах:
 ;
;




2. Определяем ток в цепи:

 .
.
3. Определяем комплексную мощность:
 ;
;
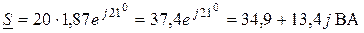 .
.
Получаем S = 37,4 ВА, Р = 34,9 Вт, Q = 13,4 ВAр (индуктивное).
Глава 6. Трехфазный ток
Трехфазная система синусоидальных токов является основной в электроснабжении промышленности и сельского хозяйства.
Трехфазные генераторы вырабатывают симметричную систему ЭДС (напряжений), одинаковых по величине и сдвинутых во времени друг относительно друга на 120 электрических градуса. Это достигается смещением обмоток (фаз) генератора в пространстве на соответствующие углы.
Применяются две основные схемы соединения фаз генератора и трехфазных потребителей: в “звезду” и в “треугольник”.
При соединении в “звезду” (рис. 6.1) концы фаз генератора (потребителя) соединяются в одну точку, которая называется нейтралью генератора (потребителя). От начал фаз генератора идут провода к потребителю, они называются линейными. Провод, соединяющий нейтрали генератора и потребителя, называется нулевым или нейтральным.
Таким образом, образуется трехфазная четырехпроводная система, наиболее распространенная. В ней различают фазные напряжения (UФ) – это напряжения между началом фазы и нейтралью (UA, UB, UC), линейные напряжения (Uл) – напряжения между линейными проводами (UAB,UBC,UCA) (рис. 14). Они опережают фазные на 300, а соотношение между ними равно:
 .
.

Рис. 6.1

Ток в линейных проводах называется линейным (Iл), в фазах генератора и потребителя – фазным (Iфг,Iфп). Для соединения в звезду фазные и линейные токи равны.
В общем случае, если сопротивления фаз потребителя различны по величине и фазе, расчет ведется для каждой фазы в отдельности по закону Ома:
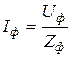 .
.
Ток в нейтральном проводе по первому закону Кирхгофа определяется векторной суммой фазных токов:
 .
.
Мощности также рассчитываются для каждой фазы:
 ;
; 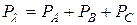 ;
;
 ;
;  ;
;

Если нагрузка симметричная (комплексные сопротивления равны по модулю и фазе), то расчет ведется для одной фазы, а мощности можно расcчитать по формулам:

 ;
;

Ток в нейтральном проводе в этом случае равен нулю.
Соединение в “треугольник” делается следующим образом (рис. 6.2) конец первой фазы соединяется с началом второй, конец второй – с началом третьей, конец третьей – с началом первой. От начала фаз генератора идут линейные провода. Так как ЭДС (напряжения) фаз генератора сдвинуты по фазе на 1200 и равны по модулю, то их векторная сумма равна нулю, и ток в фазах генератора будет определятся током потребителя.

Рис. 6.2
Как видно из схемы соединения, фазные напряжения в данном случае равны линейным:
 .
.
Фазные токи (IAB, IBC, ICA) определяются по закону Ома:
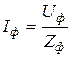 .
.
Линейные токи (IA, IB, IC) определяются по первому закону Кирхгофа для узлов А, В, С, как векторная разность соответствующих фазных токов:
узел “A”  при симметричном режиме;
при симметричном режиме;
узел “B”  ;
;  ;
;
узел “C”  .
.
Потребляемая мощность находится суммированием мощностей фаз (как при “звезде”). При симметричной нагрузке формулы для мощности те же самые, что и для соединения в “звезду”.
При включении в трехфазную сеть нескольких потребителей (рис. 6.3) результирующие линейные токи находятся векторным сложением линейных токов потребителей, а мощность – суммированием активных и реактивных мощностей потребителей. Рассчитывается полная мощность по известной формуле:  .
.

Рис. 6.3
Примем, что в соединении “звезда” нагрузка чисто активная и несимметричная, то есть  rA ¹ rB ¹ rC, а в “треугольнике” имеется активно-индуктивная симметричная нагрузка
rA ¹ rB ¹ rC, а в “треугольнике” имеется активно-индуктивная симметричная нагрузка  . Тогда фазные токи в “звезде” будут по величине различны, а по фазе совпадать со своими фазными напряжениями (UA, UB, UC). Значение тока в нейтрали найдем векторным сложением фазных токов “звезды”. Фазные токи потребителя, соединенного в “треугольник”, отстают от соответствующих фазных напряжений (UAB, UBC, UCA) на угол j.
. Тогда фазные токи в “звезде” будут по величине различны, а по фазе совпадать со своими фазными напряжениями (UA, UB, UC). Значение тока в нейтрали найдем векторным сложением фазных токов “звезды”. Фазные токи потребителя, соединенного в “треугольник”, отстают от соответствующих фазных напряжений (UAB, UBC, UCA) на угол j.
Определив числовые значения фазных токов, линейные токи IAD, IBD, ICD находим векторным построением, а затем так же векторно суммируем их с токами потребителя, соединенного в “звезду”, и находим результирующие линейные токи (рис. 6.4).

Рис. 18
В практических инженерных работах используется, как правило, символический метод.
Примеры решения задач
6.1. Определите ток в нейтральном проводе, если Ia =10 А, Iв =10 А, Ic = 6 А.
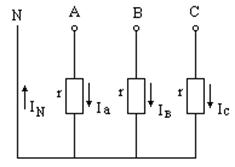
Рис. 6.1
Решение. Строим векторную диаграмму напряжений и токов. Так как сопротивления активные, то напряжения и токи совпадают по фазе и сдвинуты на 1200, а ток в нейтрале равен векторной сумме фазных токов:  . Сначала складываем токи
. Сначала складываем токи  . При этом образуется равносторонний треугольник: токи Ia и Iв равны, а угол при вершине 600, следовательно вектор
. При этом образуется равносторонний треугольник: токи Ia и Iв равны, а угол при вершине 600, следовательно вектор  , а угол между ним и током Iс равен 1800, т.е. эти векторы расположены на одной прямой и имеют противоположные направления. Поэтому IN = 10 – 6 = 4 А (диаграмма 3).
, а угол между ним и током Iс равен 1800, т.е. эти векторы расположены на одной прямой и имеют противоположные направления. Поэтому IN = 10 – 6 = 4 А (диаграмма 3).
Примечание. Если бы все токи были одинаковы, то IN = 0 (симметричная нагрузка).

6.2. Определить ток в нейтральном проводе, если Ia = Iв = Ic = 10 А.

Рис. 6.2
Решение. Хотя фазные токи равны по модулю, но эта нагрузка не симметричная: в фазе «а» ток совпадает с напряжением, в фазе «в» отстает от него на 900, а в фазе «с» опережает напряжение на 900. С учетом этого строим векторную диаграмму и определяем ток в нейтральном проводе как векторную сумму фазных токов:  .
.
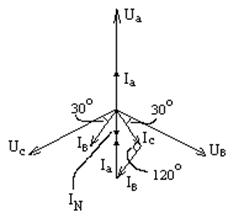
Анализ построения показывает, что [  +
+ 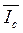 ] находится в противофазе относительно Ia, т.е. сдвиг по фазе между ними равен 1800, и количественно в
] находится в противофазе относительно Ia, т.е. сдвиг по фазе между ними равен 1800, и количественно в  раз больше фазных токов (в треугольнике векторов
раз больше фазных токов (в треугольнике векторов  ,
, 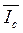 , [
, [  +
+  ] угол при вершине равен 1200) по теореме косинусов:
] угол при вершине равен 1200) по теореме косинусов:
[  +
+  ] =
] = 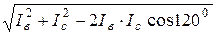 , [
, [  +
+  ] =
] =  · 10 = 17,3 А, а
· 10 = 17,3 А, а
IN = 17,3 – 10 = 7,3 А.
Аналогичный результат получается при символическом изображении токов. Если комплекс тока Ia считать вещественным положительным числом:  = Iae jo, то
= Iae jo, то 
 .
.
6.3. Все амперметры кроме двух показывают одинаковую величину тока 10 А. Какие амперметры показывают другие значения тока и сколько?
Р е ш е н и е. Анализируем схему. Имеем трехфазную, четырехпроводную систему переменного тока. Все резисторы имеют одинаковое сопротивление r и все подключены на фазное напряжение (фаза – ноль). Напряжения одинаковы по модулю и сдвинуты друг относительно друга на 1200.
Начиная с конца схемы будем исключать амперметры, показания которых заведомо одинаковые. Во-первых, это амперметры в цепи каждого резистора, т.е. амперметры 5, 6, 7, 8. Кроме того, 12 и 2 включены последовательно с 5-м, а 4-й последовательно с 6-м, а 1-й последовательно с 7-м. Эти амперметры также покажут 10 А.
Через 3-й амперметр ток идет к двум резисторам, включенным параллельно. Значит, этот амперметр покажет 20 А. Теперь разберемся с амперметрами в нейтральном (нулевом) проводе.
Через 11-й амперметр проходят два тока: с фазы «С» и фазы «В». Эти токи сдвинуты по фазе на 1200. Складывая их векторы, получим также 10 А. Через 10-й амперметр проходят три тока от трех фаз. Векторная сумма одинаковых по модулю токов, сдвинутых по фазе на 1200, равна нулю, т.е. 10-й амперметр показывает ноль. Остается 9-й амперметр. Через него кроме трех предыдущих токов проходит еще ток 8-го амперметра. Значит, он покажет тоже 10 А.

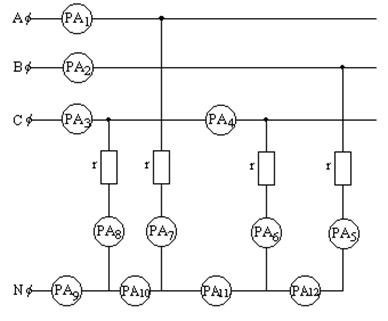
Рис. 6.3
6.4. К трехфазной линии с линейным напряжением Uл подключены трехфазный симметричный приемник, соединенный по схеме «треугольник», и группа однофазных приемников, соединенных по схеме "звезда" с нейтральным проводом. Полное сопротивление фазы симметричного приемника задано в комплексной форме:  . Мощности, потребляемые однофазными приемниками, равны РА, Рв, РС при соsφ = 1. Сопротивление нейтрального провода ZN пренебрежимо мало.
. Мощности, потребляемые однофазными приемниками, равны РА, Рв, РС при соsφ = 1. Сопротивление нейтрального провода ZN пренебрежимо мало.
Определить токи в фазах и в нейтральном проводе.
Дано: Uл = 220 В;
Zф = 11  ;
;
РА = 1200 Вт;
РВ = 2400 Вт;
РС = 3600 Вт.
Решение. Находим токи у потребителей, соединенных в «звезду» (Y). Имея в виду, что фазное напряжение в  раз меньше линейного:
раз меньше линейного:  , фазные токи определим по формуле:
, фазные токи определим по формуле:  .
.
Имеем 



Так как в соединении «звезда» потребляется только активная мощность, то сопротивление считается идеальным активным, токи совпадают по фазе с напряжениями.
Ток в нейтральном проводе находим по первому закону Кирхгофа:
 .
.
Сделав это построение в масштабе, находим:
IN = 16 A.
Для треугольника Uл = Uф, фазные токи находим по закону Ома  , а линейные токи построением:
, а линейные токи построением:
 ;
;
 ;
;
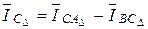 .
.
Так как нагрузка симметричная, а сопротивление имеет активно-индуктивный характер, фазные токи отстают от соответствующих напряжений на угол φ.
Находим фазные токи:

При симметричной нагрузке:
 .
.
 (это значение проверим построением векторов фазных токов и убедимся в его правильности). Показания амперметров находим векторным суммированием токов к потребителям:
(это значение проверим построением векторов фазных токов и убедимся в его правильности). Показания амперметров находим векторным суммированием токов к потребителям:
 .
.
Получаем: IC = 60 A;
IB = 50 A;
IА = 45 A.
Конечно, точность расчета при графическом решении гораздо меньше, чем при решении символически методом.
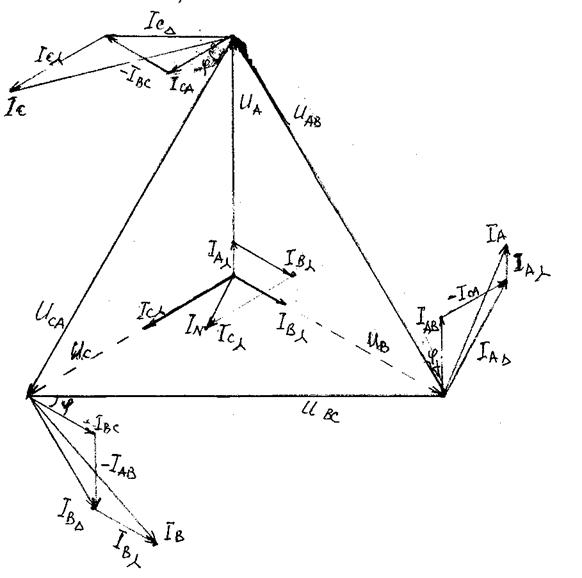
Рис. 6.4
Глава 7. Механическая характеристика асинхронного двигателя
Построение механической характеристики асинхронных двигателей по паспортным и каталожным данным обычно осуществляется по приближенной формуле:
 .
.
Эта формула дает достаточно точные результаты при изменении скольжения от нуля до критического значения. Но при достаточно больших скольжениях (0,5 и более) погрешность большая.
Поэтому построение рационально делать по следующим точкам:
1) S = 0, M = 0; 2) S = Sн, М = Мн; 3) S = Sкр, M = Mкр; затем задаться двумя значениями скольжения немного меньше и больше критического и рассчитать значения крутящего момента для них. И, наконец, при S = 1 имеем М = Мпуск.
Максимальный и пусковой моменты рассчитываются по их кратности по отношению к номинальному моменту (Мпуск /Мн, Mкр /Mн), которые приводятся в каталожных данных. Номинальный момент определяется по паспортным данным двигателя:
Мн = Рн ∙ ωн,
где Рн – номинальная мощность;
ωн = πпн/30 – номинальная угловая частота вращения, с-1;
пн – номинальная частота вращения, об/мин.
По паспортным и каталожным данным двигателя можно определить не только его механическую характеристику, но и электрические параметры, которые необходимо знать для выбора сечения проводов, пусковой и защитной аппаратуры:
1) потребляемую мощность Р1:
 ,
,
где ηн – номинальный КПД двигателя;
2) потери мощности (∆Р):
∆Р = Р1 – Рн =  ;
;
3) номинальный ток Iн:
 ;
;
4) пусковой ток Iпуск:
Iпуск = кi ∙ Iн,
где кi = Iпуск /Iн – кратность пускового тока (каталожные данные).
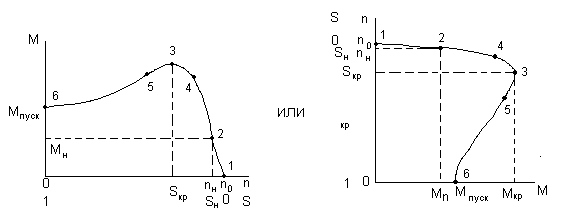
По общему виду механической характеристики можно отметить основные ее свойства.
На участке 1-2-4 (примерно до 0,8 Мкр) характеристика жесткая, т.е. при изменении нагрузки (момента) частота вращения снижается незначительно. Этот участок является рабочей частью характеристики. Работая на нем, двигатель может значительно перегружаться по моменту (по сравнению с номинальным). При этом надо иметь в виду, что момент двигателя пропорционален квадрату напряжения. При снижении напряжения сети на 10%, что допустимо нормами, его момент будет составлять (0,9)2 расчетного момента, т.е. уменьшится почти на 20% и двигатель может «опрокинуться» при работе под нагрузкой или не запуститься при пуске из-за соответствующего снижения пускового момента.
 |
Недостатком асинхронного короткозамкнутого двигателя является то, что пусковой ток в 5-7 раз превышает номинальный, что ухудшает условия пуска и работу защитных устройств, от коротких замыканий, т.к. приходится минимум в два раза завышать их ток срабатывания, чтобы избежать ложное срабатывание защиты при пуске двигателя.
Примеры решения задач
7.1.Трехфазный асинхронный двигатель с короткозамкнутым ротором питается от сети с линейным напряжением 380 В. Величины, характеризующие номинальный режим электродвигателя: мощность на валу P2н; частота вращения ротора n2н; коэффициент мощности cosj1н; КПД hн. Обмотки фаз статора соединены по схеме «звезда». Кратность критического момента относительно номинального
Ккр = Мкр /Мн.
Определить: а) номинальный и пусковой токи; б) номинальный, критический момент; в) пользуясь формулой критический и пусковой моменты:


 ;
;
Построить механическую характеристику двигателя.
ж) значения моментов, соответствующие значениям скольжения: Sн; Sk; 0,1; 0,2; 0,4; 0,6; 0,8; 1,0 (по формуле п. е.); з) пусковой момент при снижении напряжения в сети на 10 %. Построить механическую характеристику электродвигателя n = f(М).
Дано: Двигатель 4А112М2, Рн = 7,5 кВт, ηн = 87,5, cosφн = 0,88, Sн = 2,5, Sкр=17.
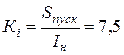 ,
,  ,
,  .
.
1. Определим номинальный ток в фазе обмотки статора:
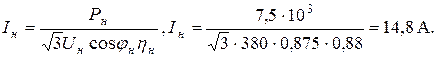
2. Число пар полюсов обмотки статора указано в обозначении типа двигателя и равно: 2р = 2, р = 1.
3. Номинальное и критическое скольжение (из таблицы): Sн = 0,025; Skр=0,17.
4. Номинальный момент на валу:
 ;
;
п = п1(1 – Sн),
где n1 – частота вращения магнитного поля статора, определяемая по формуле:

где р – число пар полюсов (для нашего двигателя р = 1),
f – частота тока (50 Гц)
имеем 
пн = 3000(1 – 0,025) = 2925 об/мин.;
 .
.
5. Максимальный (критический) момент:
 ;
;
Мкр = Мн · Ккр;
Мкр = 24,5 • 2,8 = 68,9 Н∙м.
6. Пусковой момент:
 ;
;
Мпуск = Мн · Кпуск, Мпуск = 24,5 · 2 = 49 Н∙м.
При снижении напряжения в сети на 10 % (при U = 0,9 ∙ Uн) имеем:
 .
.
7. Построим механическую характеристику: S = φ(М).
8.  ; Мкр = 68,6 Н∙м; Sн = 0,025; Skр = 0,17; 2Мкр= 137,2 Н∙м.
; Мкр = 68,6 Н∙м; Sн = 0,025; Skр = 0,17; 2Мкр= 137,2 Н∙м.
| Типоразмер электродвигателя | Основные технические данные электродвигателей | |||||||
| Мощность Pн, кВт | КПД hн, % | Коэффициент мощности cosjн | Номинальное скольжение Sн, % | Критическое скольжение Skр, % | Кратность пускового тока Iпуск / Iн | Кратность пускового момента Mпуск / Mн | Перегрузочная способность Mмакс / Mн | |
| 4А112M2 | 7,5 | 87,5 | 0,88 | 2,5 | 17,0 | 7,5 | 2,0 | 2,8 |
Р е ш е н и е:
| S | Sн = 0,025 | 0,1 | Sкр = 0,17 | 0,2 | ||
| М, Н∙м | Мн = 24,5 | 68,6 | 67,6 | Мпуск = 49 |
Дата добавления: 2014-12-23; просмотров: 1371; Мы поможем в написании вашей работы!; Нарушение авторских прав |