Смешанное соединение 2 страница

Каждому мгновенному значению синусоидального на­пряжения (синусоида 4) соответствует согласно ВАХ цепи определенное мгновенное значение тока (кривая 5). Вы­полняя построение для различных моментов времени (t₁, t₂, t₃ …), получаем график мгновенных значении тока в ви­де положительной синусоидальной полуволны тока. При положительной полуволне синусоидального напряжения (и > 0) ток в сопротивлении нагрузки есть, при отрица­тельной тока в цепи нет.

Основной величиной, ха­рактеризующей выпрямитель, является среднее значение выпрямленного тока I_d (напряжение U_d = I_dR_н). Для однополупериодного выпрямления среднее значение тока равно:

.

Важное значение при выпрямлении имеют пульсации выпрямленного тока и обратное напряжение.

Пульсации выпрямленного тока характеризуются коэф­фициентом пульсаций:

d_п = I_1m/I₀,

где I_1m – амплитуда первой гармоники пульсирующего тока, которая находится разложением функции i(t) в ряд Фурье;

I₀ – постоянная составляющая выпрямленного тока (среднее значение тока).

При однополупериодном выпрямлении d_п = 1,57.

Обратное напряжение U_обр – это максимальное напряжение на вентиле в те полупериоды, когда ток равен нулю (вентиль закрыт). Если U_обр больше допустимого для дан­ного вентиля, то последний может быть пробит. При однополупериодном выпрямлении U_обр = U_m, где U_m – ампли­туда напряжения питания.

4.3. Двухполупериодное выпрямление

При однополу­периодном выпрямлении полезно используется только один полупериод синусоидального напряжения, и поэтому зна­чительны пульсации выпрямленного тока. Эти недостатки частично устраняются в схемах двухполупериодного вы­прямления. Наибольшее применение получили две схемы: схема с нулевой точкой и мостовая схема.

Схема выпрямителя с нулевой точкой изображена на рисунке 4.4.

Рис. 4.4

Она имеет трансформатор Т и вентили VI и V2, подключенные к крайним выводам вторичной обмотки трансформатора. Сопротивление нагрузки выпрямителя R_н включено между средней точкой вторичной обмотки трансформатора и общей точкой вентилей. В тот полупе­риод, когда напряжение на половине вторичной обмотки и > 0, ток i₁ в верхнем контуре (показан штри­ховой линией) есть, а в нижнем i₂ = 0 (открыт вентиль V1, закрыт вентиль V2). В следующий полупериод u < 0 и i₁ = 0, а i₂ 0. В течение обоих полупериодов ток в нагруз­ке имеет одно и то же направление. График выпрямлен­ного тока представлен на рисунке 4.4 справа. Среднее значение выпрямленного тока вдвое больше, чем при однополупериодном выпрямлении: I₀ = 2 I_m / π = 0,637 I_m. Пульсации на­пряжения значительно меньше, чем при однополупериодном выпрямлении, коэффициент пульсаций d_п = 0,66, но обратное напряжение U_обр = 2 U_m, где U_m – амплитуда напряжения и между выводом и средней точкой вторичной обмотки трансформатора и максимальное напряжение на нагрузке.

Мостовая схема может быть собрана без трансформатора, но у нее должно быть четыре вентиля. Путь тока в один полупериод (u > 0) показан штриховой линией (через вентили VI и V3 и нагрузку). В другой полу­период (u < 0) ток протекает через вентили V2, V4 и нагрузку. В оба полупериода ток в нагрузке имеет одно и то же направление. График выпрямленного тока тот же, что и в схеме рисунка 4.4, поэтому I₀ = 0,637I_m и d_п = 0,66, но обратное на­пряжение на каждом из вентилей вдвое меньше, чем в схеме с нулевой точкой.

Рис. 4.5

4.5. Трехфазные вы­прямители

При питании от трехфазной сети при­меняются две схемы вы­прямления: с нулевой точкой и мостовая.

Для схемы с нулевой точкой нужны три венти­ля. Каждый вентиль открыт в тот ин­тервал времени, когда по­ложительное напряжение на нем больше, чем на других (например, вентиль V1 открыт при и_А > и_В и u_a >u_c), т.е. вентили открываются поочередно, а ток i в нагрузке имеет все время одно и то же направление. Среднее значение напряжения в этой схеме равно:

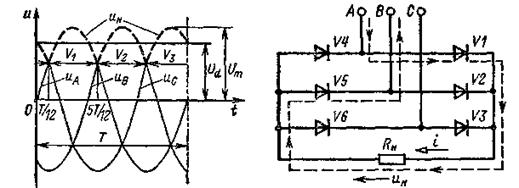
Рис. 4.6

Коэффициент пульсаций d_п = 0,25. Обратное напряже­ние U_обр равно линейному напряжению.

В мостовой схеме, называемой по имени ее автора – схе­мой Ларионова, шесть вентилей, вентили по­парно включаются на линейное напряжение, причем в от­личие от предыдущей схемы нейтрального провода нет. Графики фазных напряжений u_A = U_m sinωt, u_в = U_m sin (ωt – 120⁰), uc = U_m sin(ωt – 240⁰) показаны на рисунке 4.6.

Рис. 4.7

В каждый момент времени в одной группе вен­тилей (VI, V2, V3) открыт тот вентиль, положительный потенциал на котором больше, чем на двух других, а в дру­гой группе (V4, V5, V6) – тот, отрицательный потенциал на котором наименьший.

В интервалы времени, соответствующие фазе ωt = 30-90⁰, открыты вентили V1 и V5 (цепь тока при этом по­казана штриховой линией), при ωt = 90-150⁰ – вентили VI и V6 и т. д. Напряжение на нагрузке и_н равно линей­ному напряжению между соответствующими фазами (и_АВ при ωt = 30-90⁰). Из графика следует, что среднее значе­ние выпрямленного напряжения значительно больше, чем в схеме с тремя вентилями: , где U_m – амплитудное значение фазного напряжения, а пульсации меньше (d_п = 0,057).

4.5. Фильтры

Во всех рассмотренных схемах выпрям­ленное напряжение пульсирующее, т. е. имеет не только постоянную составляющую, но и переменную, состоящую из ряда гармонических составляющих различных частот. Для уменьшения нежелательных гармонических составля­ющих на выходе выпрямителя ставят электрические сгла­живающие низкочастотные фильтры. Схемы простейших фильтров (емкостного, индуктивного, Г-образного и П-об­разного) представлены на рисунках 4.8а-г.

Рис. 4.8

Принцип работы фильтров основан на различной зависимости реактивных сопро­тивлений от частоты. Индуктивное сопротивление для k-й гармоники X_Lk = =k_ω1L, емкостное сопротивление X_Ck = 1/ k_ω1C, т.е. индуктивное сопротивление тем больше, чем выше номер гармоники (увеличивается с ростом частоты), а емкостное меньше. Конденсатор включается парал­лельно сопротивлению нагрузки (рис. 4.8а). Для посто­янной составляющей тока емкостное сопротивление беско­нечно большое (ω = 0), поэтому постоянная составляющая тока замыкается через сопротивление нагрузки. Для гар­монических составляющих тока емкостное сопротивление уменьшается с увеличением номера гармоники (частоты). Поэтому чем больше частота, тем больший ток в емкости и меньший в сопротивлении нагрузки. Катушка индук­тивности, активное сопротивление которой должно быть по возможности минимальным, включается последователь­но в цепь нагрузки (рис.4.8б). Для постоянной состав­ляющей индуктивное сопротивление равно нулю, а для переменной тем больше, чем больше частота гармоники. Переменная составляющая ограничивается и пульсации тока уменьшаются. На рисунках 4.8в и г показаны схемы комбинированных L, С-фильтров.

Примеры решения задач

4.1. Определите средние значения выпрямленных тока I₀ и напряжения U₀, а также мощность Р, выделяемую в нагрузоч­ном резисторе R_н, обусловленную этим током, для однополупериодного выпрямителя, собранного на полупроводниковом диоде (рис. 4.1а), если его сопротивление в проводящем прямом направлении R_пр = = 5 Ом, а в непроводящем (обратном) направлении R_обр = 1000 Ом, сопротивление нагрузочного резис­тора R_н = 400 Ом, напряжение питающей сети U = 220 В. Вольтамперная характеристика электрической цепи приведена на рисунке 4.1б, нелинейностью характеристики пренебречь.

Рис. 4.1

Р е ш е н и е. Сопротивление электрической цепи:

в проводящий (прямой) полупериод: R₁ = R_пр + R_н = 5 + 400 = 405 Ом;

в непроводящий (обратный) полупериод: R₂ = R_обр + R_н = 1000 + 400 = 1400 Ом.

Амплитудное значение напряжения питающей сети:

Амплитудное значение тока цепи:

в проводящий полупериод: I ^'_т = U_m /R₁ = 310,2/405 = 0,766 А;

в непроводящий полупериод: I ^''_т = U_m /R₂ = 310,2/1400 = 0,222 А.

Постоянные составляющие:

прямого тока: I^'₀ = I^'_т/π = 0,766/3,14 = 0,244 А;

обратного тока: А.

Средние значения:

выпрямленного тока: I₀ = I ^'₀ – I ^''₀ = 0,244 – 0,071 = 0,173 А;

выпрямленного напряжения: U₀ = R_н I₀ = 400 ∙ 0,173 = 69,2 В.

Мощность, выделяемая в сопротивлении резистора, обуслов­ленная постоянной составляющей выпрямленного тока: (0,173)² 400 = 11,972 Вт.

4.2. Определите действующее U₂ и амплитудное U_2m значения напряжения на вторичной обмотке трансформатора, его коэф­фициент трансформации п, постоянную составляющую выпрям­ленного тока I₀; выберите полупроводниковые вентили для двухполупериодного выпрямителя, выполненного по мостовой схеме рисунке 4.2. Выпрямленное напряжение U₀ = 350 В на нагрузочном резисторе R_н = 1400 Ом, напряжение питающей сети U₁ = 127 В.

Рис. 4.2

Р е ш е н и е. Действующее значение напряжения на вторич­ной обмотке трансформатора в данной схеме выпрямления:

В. Коэффициент транс­формации трансформатора: n = U₁ / U₂ = 127 / 390 = 0,333.

Амплитудное значение напряжения на вторичной обмотке трансформатора: U_m2 = U₂ = 1,41 ∙ 390 = 549,9 В.

Значение максимального обратного напряжения вентиля в данной мостовой схеме: U_{обр max} = U_m2 = 549,9 ≈ 550 В.

Постоянная составляющая выпрям­ленного тока: I₀ = U₀ /R_н = 350/1400 = 0,25 А.

По справочнику, исходя из расчет­ного значения тока I₀ и значения об­ратного напряжения U_{обр max}, выбираем вентили типа Д7Ж с номинальными данными: током I₀ = 0,3 А и макси­мальным допустимым обратным напря­жением вентиля U_{обр max B} = 400 В.

Число последовательно включенных вентилей в плече мос­товой схемы: N U_{обр max} / U_{обр max B} = 550/400 = 1,38. Принимаем N = 2.

4.3. По условию предыдущей задачи определите максимальные значе­ния I_2т выпрямленного тока, напряжения U_2m и мощность Р, выделяемую в сопротивлении нагрузочного резистора R_н.

Р е ш е н и е. Значение выпрямленного тока: I₀ = U₀ /R_н = 350/1400 = 0,25 А.

Амплитудные значения:

выпрямленного тока: А;

выпрямленного напряжения: В или

U_2m = R_н I_2m = 1400 ∙ 0,393 = 550 В.

Мощность, выделяемая в сопротивлении нагрузочного резис­тора:

Р = U₀ I₀ = 350 ∙ 0,25 = 87,5 Вт или P = R_н = 0,25² · 1400 = 87,5 Вт.

4.4. Пользуясь входными и выходными характеристиками транзистора типа П210Б-П210В (рис. 4.3а, б), включенными по схеме с общим эмиттером (ОЭ), определить h-параметры для точки 1 с координатами U_к1 = -4,5 В, I_б1 = 47 мА. Нели­нейностью характеристик на рассматриваемом участке прене­бречь.

Рис. 4.3

Р е ш е н и е. Входное сопротивление транзистора:

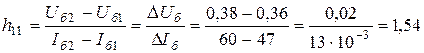Ом,

где в соответствии с входной характеристикой (рис. 4.3а), для точек 1 и 2: U_б1 = =0,36 В; U_б2 = 0,38 В; U_к1 = -4,5 В и U_к2 = -2 В; I_б1 = 47 мА; I_б2 = 60 мА.

Коэффициент обратной связи по напряжению

,

здесь ∆U_к = U_к2 – U_к1 = -2 – (-4,5) = 2,5 В; ∆U_б = U_б2 – U_б1 = 0,38 – 0,36 = 0,02 В, где в соответствии с входными характеристиками транзистора (рис. 4.3а) для точек 1 и 2 U_к2 = -2 В и U_к1 = -4,5 В при неизменном токе базы I_б2 = 60 мА.

Коэффициент передачи тока: , = 1 А, ∆I_б2 –∆I₆₁ = 100 – 50 = 50 мА = 0,05 А, где в соот­ветствии с выходной характеристикой (рис. 4.3б) транзистора при неизменном значении напряжения коллектора U_к1 = -4,5 В: I_б2 = 100 мА, I_б1 = 50 мА.

Выходная проводимость транзистора:

,

где = 0,4 А; ∆U_к = U_к2 – U_к1 = -4,5 – (-11) = 6,5 В; здесь в соответствии с выходной ха­рактеристикой транзистора (рис. 4.3б) при неизменном токе базы = 50 мА при U_к2 = -4,5 В и U_к1 = -11 В.

Глава 5. Расчет линейных электрических цепей синусоидального тока

Синусоидальный переменный ток однофазный и трехфазный получил самое широкое применение. Расчет цепей переменного тока имеет свои особенности, хотя базируется на тех же законах.

5.1. Основные понятия

Мгновенное значение (i) – величина тока в любой момент времени.

Амплитудное значение (I_m) – максимальное значение тока.

Действующее значение ( ) – величина постоянного тока, эквивалентна по тепловому действию переменному току (цепь с резистором).

Начальная фаза (y_i) – несовпадение во времени начала синусоиды и начала отсчета времени, выраженное в электрических градусах.

Сдвиг по фазе (j) – несовпадение во времени начал двух синусоид, выраженное в электрических градусах.

Период (T) – время одного полного колебания.

Частота тока (f = 1/T) – количество полных колебаний в единицу времени. Одно колебание в секунду равно одному герцу (Гц).

Угловая частота (w = 2pf) – угол поворота вектора за единицу времени. Размерность – радиан в секунду.

Эти понятия относятся и к синусоидальным ЭДС, напряжению.

Графическое изображение синусоид неудобно, поэтому синусоидальные величины представляют в виде вектора, вращающегося против часовой стрелки с угловой частотой «w». (При расчетах берут их действующие значения) (рис. 5.1).

Рис. 5.1

5.2. Виды сопротивлений на переменном токе

Наличие переменных магнитных полей и связанных с этим явлений индукции и самоиндукции, поверхностного эффекта, гистерезиса и других усложняют свойства приемников электроэнергии на переменном токе и расчет цепей.

Пренебрегая наличием определенных электромагнитных процессов из-за малости их влияния на результаты инженерных расчетов, выделяют три вида идеальных сопротивлений на переменном токе.

1. Активное сопротивление (r). В таких приемниках вся электрическая энергия необратимо превращается в другой вид энергии (в резисторах в тепловую). Идеальное активное сопротивление эквивалентно сопротивлению резистора (R) на постоянном токе. Напряжение и ток совпадают по фазе, т.е. j = 0, cosj = 1. (рис. 5.2).

U_r = I · r (закон Ома);

φ = 0.

Рис. 5.2

2. Индуктивное сопротивление (Х _L). Если из сверхпроводника (r = 0) намотать катушку и подключить к источнику синусоидального напряжения, то величина тока не будет равна бесконечности, как это следовало бы из закона Ома для постоянного тока или для идеального активного сопротивления, а будет ограничена определенным значением, т.е. в такой цепи появилось какое-то сопротивление.

Рис. 5.3

Причина этого – наводимая в катушке переменным магнитным полем ЭДС самоиндукции (e_L) (рис. 3).

По II закону Кирхгофа имеем:

u_L + e_L = 0, откуда u_L = -e_L,

так как e_L = -Ldi/dt, где L – индуктивность, то при i = I_msinwt имеем:

u_L = Ldi/dt = LwI_mcoswt = LwI_msin(wt + p/2), т.е. напряжение опережает ток на 90 электрических градусов или ток отстает от напряжения на 90⁰.

Произведение «Lw» имеет размерность сопротивления (Ом) и называется индуктивным сопротивлением:

X_L = wL.

Векторная диаграмма и закон Ома для идеального индуктивного сопротивления имеет вид (рис. 5.4):

cos = φ;

U_L = I · X_L;

(отстающий).

Рис. 5.4

3. Емкостное сопротивление (X_C).

Если к источнику синусоидального напряжения подключить конденсатор (С) (рис. 5.5), то амперметр покажет, что по этой цепи проходит ток. Это объясняется процессами зарядки и разрядки конденсатора при постоянных изменениях направления тока, т. е. заряды циркулируют по обеим полуветвям от источника и обратно, конечно, не проходя сквозь конденсатор. Это будет его пробой.

Рис. 5.5

Величина движущихся зарядов (q) определяется выражениями:

q = idt = Cdu_C, откуда i = Cdu_C/dt;

при u_C = U_m sinwt имеем:

i = CdU_msinwt/dt = CwU_mcoswt = CwU_msin(wt + p/2),

т.е. в конденсаторе ток опережает напряжение на угол p/2 (рис. 5.6). Произведение «Сw» имеет размерность Ом^-1 = См – (симменс), отсюда 1/Cw = X_C называют емкостным сопротивлением.

Для такого идеального сопротивления имеем:

U_C = I · X_C;

(опережающий).

Рис. 5.6

Реальные приемники на переменном токе обладают одновременно всеми свойствами идеальных сопротивлений, и их схемы замещения можно представить как последовательное или параллельное соединение идеальных активных сопротивлений (r) и реактивных (X_L и X_C).

5.3. Последовательное соединение r, L, C элементов. Закон Ома

Второй закон Кирхгофа для данной цепи с последовательным соединением r-, L-, C-элементов (рис. 5.7), при векторном изображении величин будет выглядеть следующим образом:

Рис. 5.7

Строим векторную диаграмму (рис. 5.8), проводя операцию сложения векторов. За базовый вектор возьмем ток, так как при последовательном соединении он один. Получили треугольник напряжений из которого, зная значения составляющих напряжений, можно найти:

;

.

Рис. 5.8

Разделив стороны этого треугольника на ток, получим подобный треугольник, отражающий наличие и величины сопротивлений в данной цепи (рис. 5.9).

Рис. 5.9

Здесь Z=U/I называется полным сопротивлением и определяется выражением:

.

Сдвиг по фазе между током и общим напряжением можно также найти из треугольника сопротивлений:

.

При положительном тангенсе ток отстает от напряжения, при отрицательном опережает его.

С учетом изложенного закон Ома для последовательного соединения имеет вид (в общем случае):

.

Однотипные сопротивления складываются арифметически.

5.4. Параллельное соединение r-, L-, C-элементов.

Зная закон Ома для последовательного соединения элементов и I закон Кирхгофа, для цепи с последовательным соединением r-, L-, C-элементов (рис. 5.10) можно найти токи в ветвях и общий ток как векторную сумму токов ветвей:

Рис. 5.10

, (отстающий);

, (опережающий).

Строим векторную диаграмму (рис. 5.11). За базовый вектор возьмем напряжение «U», общее для ветвей.

Рис. 5.11

Для аналитического расчета рассмотрим треугольник ABC.

В нем: .

В свою очередь:

AB = AF + FB = I₁cosj₁ + I₂cosj₂;

BC = BD – CD = I₁sinj₁ - I₂sinj₂.

Проекции токов на вектор напряжения называются активными составляющими тока.

Icosj = I_a.

Проекции на ось, перпендикулярную напряжению, называются реактивными составляющими:

Isinj I_p,

тогда

;

.

Этот метод расчета называется методом активных и реактивных составляющих.

5.5. Метод проводимостей

По закону Ома I = U/Z, а из треугольника сопротивлений cosj = r/Z; sinj = X/Z, тогда

I_a = Icosj = (U/Z)(r/Z) = U(r/Z²) = Ug;

I_p = Isinj = (U/Z)(X/Z) = U(X/Z²) = Ub,

где g =r/Z² – активная проводимость ветви;

b = X/Z² – реактивная проводимость (может быть b_L и b_C).

Заменяя активные и реактивные составляющие токов, рассмотренные в предыдущем методе, получим формулы для расчета общего тока и сдвига по фазе:

,

где – полная проводимость соединения.

.

Таким образом, методика расчета заключается в определении активных и реактивных проводимостей ветвей и по соответствующим формулам расчета тока и сдвига по фазе. Однотипные проводимости складываются арифметически.