Смешанное соединение 3 страница

5.6. Резонанс в электрических цепях

Резонансом называют такой режим цепи, имеющего L и C элементы, при котором сдвиг по фазе (j) между напряжением и током равен нулю.

При последовательном соединении элементов возможен резонанс напряжений при условии X_L = X_C. Тогда Z = r, U_L = U_C, U = U_r, j = 0, cosj = 1, ток в цепи максимальный. Если реактивные сопротивления много больше активного, то на реактивных элементах появляются большие напряжения, которые значительно могут превышать напряжения сети. Это и используется для выделения полезного сигнала по напряжению. Одновременно необходимо учитывать опасность появления высоких напряжений на реактивных элементах цепи.

Резонанс напряжений возможен при любых параметрах L, C при определенной частоте тока, называемой резонансной (w_о), которая находится из условия:

X_L = X_C, w_oL = 1/w_oC,

откуда , где .

При параллельном соединении при условии b_L = b_C имеем тоже резонансные явления. При этом y =g, I_L = I_C, I = I_a, j = 0, cosj = 1, ток в цепи минимальный, в то же время токи I_L и I_C могут значительно превышать общий ток.

Это находит практическое применение в радиотехнике, а в электротехнике параллельное подключение конденсаторов к активно-индуктивной нагрузке применяется для снижения потребляемого тока и повышения cosj, имеющего важное технико-экономическое значение.

Возможность получения резонанса тока для конкретной цепи определяется не только параметрами L и C, но и активными сопротивлениями ветвей, так как от них также зависит величина реактивных проводимостей (b_L и b_C).

5.7. Мощность цепи синусоидального тока

Мгновенная мощность определяется выражением p = ui.

Для идеального активного сопротивления имеем (j = 0):

.

Найдем среднюю мощность за период:

.

Эта мощность называется активной и измеряется в ваттах (Вт). Она характеризует необратимые преобразования электрической энергии на данном участке цепи.

Для реактивных сопротивлений, учитывая, что в катушке индуктивности напряжение опережает ток на 90⁰, а в конденсаторе отстает на 90⁰ от тока, будем иметь:

;

.

В реактивных сопротивлениях мощности колеблются с двойной частотой и находятся в противофазе. Но за четверть основного периода тока мощности положительные, что означает накопление магнитной энергии в катушке или заряд конденсатора, вторую четверть они отрицательны, значит энергия отдается обратно в сеть и необратимо ни во что не превращается (средняя за период мощность равна нулю). Поэтому такая мощность называется реактивной, имеет свое обозначение (Q) и размерность – ВАр (вольт-ампер реактивный):

; ; .

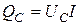Кроме активной и реактивной мощности цепи переменного тока характеризуются полной мощностью S. Это максимально возможная мощность при заданных U и I. Единица измерения – ВА (вольт-ампер). Это максимально возможная мощность при заданных U и I:

S = UI.

Рис. 5.12

Соотношение между мощностями определяется из треугольника мощностей (рис. 5.12), который можно получить из треугольников напряжений или токов.

Для расчета мощностей в зависимости от схемы соединения применяют различные формулы, вытекающие из основной:

;

;

.

5.8 Символический метод расчета цепей переменного тока

(метод комплексных чисел)

При расчетах электрических цепей переменного тока широко применяется метод комплексных чисел, позволяющий графические операции над векторами заменить алгебраическими действиями над комплексными числами.

Вектор можно однозначно отобразить на комплексной плоскости, вещественная и мнимая оси которой позволяют изобразить вектор в виде комплексного числа. В отличие от математики мнимое число обозначается буквой j (жи).

Вектор в виде комплексного числа имеет три формы записи:

а) алгебраическая ;

б) тригометрическая , где – модуль ;

в) в виде показательной функции .

В символическом методе активное сопротивление является вещественным положительным числом , индуктивное – положительным мнимым: , емкостное – отрицательным мнимым:

При использовании комплексных чисел методы расчета электрических цепей переменного тока аналогичны методам расчета; электрических цепей постоянного тока. Записи соответствующих уравнений, составленных по законам Ома и законам Кирхгофа, одинаковы по форме для электрических цепей однофазного пере­менного и постоянного токов.

При этом в уравнениях, записанных для электрических цепей переменного тока, токи , напряжения , ЭДС , сопротивле­ния , проводимости , мощности записывают в комплекс­ной форме.

С учетом этого математическое выражение закона Ома в комплексной форме приводят к виду: = / или = .

Математическое выражение первого закона Кирхгофа в комплексной форме: . В соответствии с этим алгебраическая сумма комплексных токов, сходящихся в узле разветвления электрической цепи, равна нулю.

Математическое выражение второго закона Кирхгофа в комплексной форме:

.

Согласно этому уравнению алгебраическая сумма комплексных ЭДС в любом замкнутом контуре электрической цепи равна алгебраической сумме комплексных напряжений и алгебраической сумме падений напря­жений в этом контуре.

При расчете электрических цепей по методу комплексных чи­сел оперируют с этими числами. Алгебраические действия над комплексными числами сводятся к сложению, вычитанию, умно­жению и делению комплексных чисел.

Сложение комплексных чисел осуществляется следующим образом:

.

Вычитание комплексных чисел производится аналогично:

.

Умножение комплексных чисел производится по схеме:

или .

Деление комплексных чисел осуществляется следующим об­разом:

или .

При делении комплексных чисел для исключения в знамена­теле мнимого числа числитель и знаменатель умножают на сопряженное со знаменателем комплексное число.

Примеры решения задач

5.1. Все амперметры, кроме одного, показывают 2 А. Какой амперметр показывает другое значение и сколько, если r = x_L = x_C ?

Рис. 5.1

Р е ш е н и е. Так как r, L, C-элементы включены параллельно (напряжение на них одинаково) и их сопротивления равны, то одинаково (2 А) показывают 2-й, 4-й, и 5-й амперметры. Построим векторную диаграмму, используя I закон Кирхгофа: .

Через 3-й амперметр проходят токи I_L и I_C, т.е. . Но токи в катушке и в конденсаторе друг относительно друга сдвинуты на 180⁰, поэтому их сумма равна нулю, т.е. амперметр рА₃ покажет ноль, а 1-й амперметр тоже покажет 2 А.

5.2. Определите напряжение сети, если U₁ = U₂ = U₃ = U₄ = 100 B. Определите показания 5-го вольтметра и 6-го.

Рис. 5.2

Р е ш е н и е. Имеем последовательное соединение элементов (делитель напряжения). Напряжение сети равно сумме (векторной) напряжений на участках:

= + + + .

Строим векторную диаграмму.

Таким образом, напряжение сети U = U₁ + U₃ = 200 В.

Аналогичный результат можно получить по формуле:

.

Для пятого вольтметра имеем:

= + , U₅ = 0 В.

Напряжения U₂ и U₃ равны по модулю и противоположны по фазе.

Показания шестого вольтметра определим из соотношения , построив векторную диаграмму:

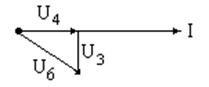
откуда ,

5.3. Определите емкость конденсатора С для получения cosφ = 1 при условии: r = 16 Ом, L = 0,0382 Гн, f = 50 Гц, U = 200 В. Как изменится потребляемый из сети ток при включении конденсатора.

Рис. 5.3

Первый вариант решения. Подключение конденсаторов параллельно активно-индуктивной нагрузке используется для повышения коэффициента мощности потребителей и уменьшения потребляемого тока путем достижения резонанса токов.

Находим:

1) индуктивное сопротивление: X_L = ωL, X_L = 0.0382 · 2π · 50 = 12 Oм;

2) полное сопротивление ветви (rL): , Ом;

3) величина тока , A и сдвиг по фазе , φ₁=37⁰ (отстающий), при этом cosφ₁ = 0,8;

4) при параллельном соединении полная проводимость у для данной схемы будет: ,

где активная проводимость См;

индуктивная проводимость См,

а для получения cosφ = 1 (резонанс токов) необходимо иметь в_L = в_C, где в_С = ωС. Отсюда находим Ф;

5) так как в_L = в_C, то у = g и потребляемый из сети ток уменьшается: I₂ = U · g, I = 200 · 0,04 = 8 A;

6) векторная диаграмма имеет вид:

Второй вариант решения. Определив ток I₁ и угол φ₁, находим активную и реактивную мощность потребителя:

Р = U∙I₁ cosφ₁, P = 200∙10∙0,8 = 1600 Вт;

Q_L = U∙I₁ sin φ₁, Q_L = 200∙10∙0,6 = 1200 ВАр.

Для получения cosφ₁ = 1 необходимо компенсировать реактивную мощность (индуктивную) соответствующей емкостной мощностью Q_C = Q_L.

Реактивная мощность конденсатора определяется выражением , где ω = 2πf.

Тогда Q_L = Q_C = U²ωC, откуда

В общем случае, если надо повысить cosφ потребителя с активно-индуктивной нагрузкой, т.е. изменить сдвиг по фазе между током и напряжением от φ₁ до φ₂, то, зная активную мощность, емкость конденсатора можно найти из треугольников мощностей:

Q_C = Q_L1 – Q_L2 = P (tg φ₁ – tg φ₂ ),

откуда .

В нашей задаче tg φ₂ = 0. Потребляемый ток будет уменьшаться, т.к. уменьшается полная мощность S.

5.4. Для цепи переменного тока с последовательным соединением r, L, C-элементов дано: U = 100 B, r = 3 Ом, x_L = 6 Ом, х_С = 2 Ом. Определите ток, напряжение на элементах и потребляемые мощности S, P, Q. Постройте комплексы напряжений. Расчет проведите символическим методом.

Рис. 5.4

Р е ш е н и е. 1. Находим комплекс полного сопротивления цепи:

,	Ом;
,	Ом;
,	;
	Ом.

1. Находим комплекс тока:

, .

2. Находим комплексы напряжений на элементах схем

,
,
,

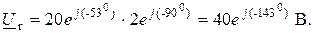
3. Находим комплекс мощности

,	;
.

Имеем S = 2000 ВА, Р = 1200 Вт, Q = 1600 ВАр (индуктивное).

Проверка сделана построением суммы комплексов напряжении:

5.5. По векторной диаграмме определите схему соединения элементов, рассчитайте их параметры, постройте треугольник мощностей.

Дано: I = 0,5 A;

U₁ = 100 B;

φ₁ = 30⁰;

U₂ = 50 B;

φ ₂ = 0;

U₃ = 125 B;

φ ₃ = 60⁰.

Рис. 5.5

Р е ш е н и е. Анализируем векторную диаграмму. Вектор тока один, а три напряжения (U₁, U₂, U₃) складываются.

Имеем последовательное соединение трех элементов: первый – реальная катушка индуктивности (r₁, L), т.к. угол φ₁ – отстающий и меньше 90⁰, второй – активное сопротивление (r₂), т.к. векторы напряжения U₁ и тока I совпадают (угол φ ₂ = 0); третий – реальный конденсатор (r₃, C), т.к. ток опережает напряжение U₃ на угол φ ₃, меньший 90⁰. Составляем схему соединения, эквивалентную векторной диаграмме

Определяем параметры схемы

1) , ;

r₁ = z₁cosφ₁, r₁ = 200cos30⁰ = 173 Ом;

х_L = z₁sinφ₁, x_L = 200sin30⁰ = 100 Ом;

2) ;

3) , ;

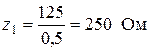r₃ = z₃cosφ₃ r₃ = 250cos60⁰ = 125 Ом;

х_С = z₃sinφ₃ x_С = 250sin60⁰ = 216 Ом.

Для построения треугольника мощностей находим P, Q, S

P = I²(r₁ + r₂ + r₃), P = 0,5²(173 + 100 + 125) = 99,5 Вт;

Q = I² (x_L – x_C), Q = 0,5² (100 – 216) = -29 ВAр,

Знак «–» показывает преобладание емкостной мощности.

В масштабе строим треугольник мощностей.

При правильном расчете и построении треугольник мощностей и треугольник напряжений 0ав подобны. Докажите это самостоятельно, определяя tgφ для этих треугольников. В треугольнике напряжений

0а = Σ U_a = I(r₁ + r₂ + r₃);

ав = Σ U_р = U_L – U_C.

5.6. По векторной диаграмме определите схему соединения элементов, рассчитайте их параметры, постройте треугольник мощностей.

Дано: U₁ = 100 B;

I₁ = 5 A;

φ₁ = 30⁰;

I₂ = 10 A;

φ ₂ = 45⁰;

I₃ = 5 А;

φ ₃ = 0.

Рис. 5.6

Р е ш е н и е. Анализируем векторную диаграмму. Вектор напряжения один, а три тока I₁, I ₂, I₃ суммируются. Имеем параллельное соединение трех ветвей. Первая – реальная катушка индуктивности (r₁L), т.к. ток I₁ отстает от напряжения, а угол φ₁ меньше 90⁰; вторая – реальный конденсатор (r₂C), т.к. ток I₂ опережает напряжение на угол φ₂ < 90⁰; третья – идеальное активное сопротивление, т.к. напряжение и ток совпадают по фазе. Составляем схему соединения, эквивалентную векторной диаграмме.

Определяем параметры схемы:

1) ;

r₁ = z₁cosφ₁, r₁ = 20cos30⁰ = 17,3 Ом;

х_L = z₁sinφ₁, x_L = 20sin30⁰ = 10 Ом;

2) , ;

r₂ = z₂cosφ₂ , r₂ = 10cos45⁰ = 7 Ом;

х_С = z₂sinφ₂, x_С = 00sin45⁰ = 7 Ом;

3) , .

Для построения треугольника мощностей находим P, Q, S, используя метод активных и реактивных составляющих или проводимостей. По первому методу имеем

Σ I_a = 5cos30⁰ + 10cos45⁰ + 5cos0⁰ = 16,4 A;

Σ I_p = I_L – I_C = I₁sinφ₁ – I₂ sinφ₂;

Σ I_p = 5sin30⁰ – 10sin45⁰ = -4,57 A.

Знак «–» показывает преобладание тока через конденсатор.

Зная активные и реактивные составляющие тока, находим мощности:

P = U ·ΣI_а P = 100 · 16,4 = 1640 Вт;

Q = U (I_L – I_C) Q = 100 (-4,57) = -457 ВAр;

В масштабе строим треугольник мощностей.

При правильном расчете и построении он подобен треугольнику токов 0ав, а тангенс угла φ должен быть равным:

,

в чем нетрудно убедиться.

5.7. Реальная катушка индуктивности включена в цепь синусоидального переменного тока с частотой f = 50 Гц. Действующее значение напряжения 450 В. Амперметр показывал I = 8 А, ваттметр Р = 2000 Вт. Какую емкость конденсатора С необходимо включить для получения резонанса токов, и как изменится величина потребляемого из сети тока?

Рис. 5.7

Р е ш е н и е. Реальная катушка является активно-индуктивным сопротивлением, в ней ток отстает от напряжения на угол φ, который меньше 90⁰. Коэффициент мощности таких потребителей низкий cosφ < 1 (электрические двигатели, сварочные аппараты, люминесцентные лампы и др.). Включая параллельно катушке конденсатор, ток в котором опережает напряжение на 90⁰, мы можем значительно снизить потребляемый ток и повысить cosφ. При резонансе токов cosφ = 1.