
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Сепарационные характеристики и границы разделения
Остановимся подробней на отличительных особенностях задания фракционного состава и сепарационных характеристик информационных методов обогащения. Они отличаются большим разнообразием.
Имеет отличительные особенности и сепарационная характеристика, присущая аппаратам информационных методов обогащения. Сепарацию можно рассматривать как последовательность двух операций. Первая – это определение значения признака разделения частицы и принятие решения об удалении, вторая – удаление частицы из потока.
Вероятность отнесения частицы с истинным значением признака разделения к хвостам или концентрату по результатам измерения этого признака зависит, во-первых, от совершенства измерительной и питающей системы, и, во-вторых, от настройки сепаратора, то есть от заданной ξгр
(рис. 5.6, а-в).
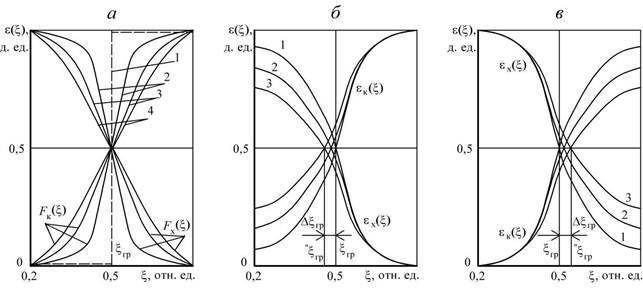
Рис. 5.6. Сепарационные характеристики информационных сепараторов при различных сочетаниях погрешностей измерения и отбора:
а – при P=0, S: 1 – 0; 2 – 0,05; 3 – 0,10; 4 – 0,15;
б – при S =0,10, Pп: 1 – 0,95; 2 – 0,85; 3 – 0,75 (удаляемый продукт – хвосты);
в – при S =0,10, Pм: 1 – 0,95; 2 – 0,85; 3 – 0,75 (удаляемый продукт – концентрат)
Эта вероятность определяется по эталонировочным кривым, отличающимся видом аналитической аппроксимации в зависимости от
применяемого метода. Иногда (для числа регистрируемых элементарных частиц от куска радиоактивной руды менее 20) используют распределение Пуассона. Чаще (для большинства методов и большом числе регистрируемых элементарных частиц от куска руды) оценка вероятности отнесения кусков к концентрату или хвостам производится на основе закона нормального распределения Гаусса. Поэтому дальнейший анализ проведем при использовании в качестве вероятностной характеристики опознания интегральной кривой нормального закона распределения F(ξ), которая количественно оценивается средним квадратичным отклонением S, и настройкой сепаратора, то есть ξгр (рис. 5.6, а). Более совершенный сепаратор малое имеет значение S, а потому более крутую характеристику в точке перегиба при ξгр. Идеально измеряющий и принимающий решение сепаратор имеет ступенчатую характеристику опознания кусков. Сумма вероятностей отнесения частицы к хвостам, либо к концентрату равна 1. Поэтому
FX(ξ) = 1–FК(ξ).
Именно эталонировочными кривыми пользовались как инструментом прогноза в информационных методах обогащения. Поскольку сама сепарация – это не только информационные процедуры, но и механическое удаление частиц, в истинной сепарационной характеристике, в отличие от эталонировочных кривых, необходим учет этой составляющей.
Вторая операция – удаление (отбор) кусков, так же как и идентификация, вносит свою погрешность в разделение. В данном случае ошибки возникают вследствие сбоев в удаляющей системе, в системе подачи материала (сдвоенные куски) и т. п. В простейшем случае можно допустить, что не подлежащие удалению куски всегда попадают в нужный продукт при нормальной регулировке механической части сепаратора, а подлежащие удалению – имеют большую вероятность быть удаленными, но сохраняют некоторую вероятность неудаления. Вероятность правильного отбора Р не зависит от значения признака разделения куска.
Сепарационная характеристика информационного сепаратора, если бедные куски имеют меньшее, а богатые большее значение ξ, может быть определена как произведение вероятностей последовательности операций по формулам:
при удалении богатых полезным минералом кусков:
для концентрата (удаляемый продукт)
| м | (x)= P Fк (x), | ||||||
| eк | (5.1) | ||||||
| для хвостов (неудаляемый продукт) | |||||||
| eм (ξ) = 1 - F | (ξ)+ F | (ξ)(1 - Р) = 1 - Р F | (ξ) | (5.2) | |||
| х | к | к | к | ||||
при удалении бедных (породных) кусков:
для хвостов (удаляемый продукт)
| п | |||
| eх (x)= Р [1- Fк (x)], | |||
| для концентрата (неудаляемый продукт) | |||
| п | (x)= Fк (x)+ [1- Fк (x)](1- Р)=1 | - Р + Fк (x) Р , | |
| eк |
(5.3)
(5.4)
где Fк(ξ)– интегральная функция распределения вероятности отнесения куска к концентрату при идентификации; P– вероятность правильного удаления при отборе либо богатых, либо бедных минералом кусков (приняты одинаковыми).
Заметим, что
εмк (ξ)+ εмх (ξ)=1, εпк (ξ)+ εпх (ξ)=1.
Тогда из сопоставления формул (5.1) и (5.3), (5.2) и (5.4) следует, что при удалении из потока богатых или бедных кусков и одинаковой точности идентификации сепарационные характеристики для концентрата и хвостов отличаются друг от друга (рис. 5.6, б, в). При этом происходит смещение границы разделения.
В более общем случае, помимо неэффективного удаления кусков, вероятен попутный выброс в удаляемый продукт кусков, не подлежащих удалению, например, при прохождении близкорасположенных кусков друг к другу, один из которых бедный, а другой богатый, удаляющее воздействие переместит оба куска в удаляемый продукт. Вероятность этого возрастает при увеличении частоты подачи. То есть, возможно как неудаление требующих удаления кусков с вероятностью (1-P), так и удаление не подлежащих удалению кусков с вероятностями (1-R), где R – вероятность правильного неудаления. Тогда сепарационная характеристика аппарата с идеальной измерительной системой будет иметь вид, меняющийся с изменением вида выделяемого продукта, (рис. 5.7) и описываться выражениями (5.5)-(5.8).

Рис. 5.7. Сепарационные характеристики информационного сепаратора при идеальном измерении признака разделения и погрешностях удаления в оба разделяемых продукта:
а – удаление в выделяемый продукт (концентрат) богатых полезным минералом кусков;
б – удаление в выделяемый продукт (хвосты) породных кусков
при удалении богатых кусков:
| 1- R | при | ξ < ξгр | ; | |
| εкм (ξ)= | 0,5 | при | ξ = ξгр ; | (5.5) |
| P, | при | ξ > ξгр . | ||
| R | при | ξ < ξгр ; | ||
| εмх (ξ)= | 0,5 | при | ξ = ξгр ; | (5.6) |
| 1- P, | при | ξ > ξгр. |



при удалении бедных кусков:
| P | при | ξ < ξгр | ; | (5.7) | ||
| εПх (ξ)= | ||||||
| 0,5 | при | ξ = ξгр ; | ||||
| 1- R, | при | ξ > ξгр. | ||||
| 1- P | при | ξ < ξгр ; | (5.8) | |||
| εкП (ξ)= | ||||||
| 0,5 | при | ξ = ξгр ; |
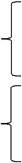


R, при ξ > ξгр .
Если перейти к более общему случаю, когда существуют погрешности и удаления, и неудаления, а также функция погрешностей измерения F (описываемая, например, интегральной кривой вероятности Гаусса), графики сепарационных характеристик для разных случаев, примут вид, показанный на рис. 5.8.
Выражения, описывающие сепарационные характеристики, тогда будут следующими:
| εкм = 1 - R + (P + R -1) F; | (5.9) |
| м | (5.10) |
| εх = R - (P + R -1) F; | |
| εхП = P - (P + R -1) F; | (5.11) |
| εкП = 1 - P + (P + R -1) F. | (5.12) |




Из приведѐнных формул следует, что, если P≠R, то следует ожидать разных технологических показателей информационного разделения при выделении в удаляемый продукт богатых минералом или породных кусков. Границы разделения для этих случаев также будут различными.

Рис. 5.8. Сепарационные характеристики информационного сепаратора при погрешностях измерения и удаления в оба разделяемых продукта:
а – удаление в выделяемый продукт (концентрат) богатых полезным минералом кусков;
б – удаление в выделяемый продукт (хвосты) породных кусков
Кроме перечисленных погрешностей вид сепарационной характеристики зависит от содержания компонентов в кусках, которые при различных методах измерения могут идентифицироваться, начиная с различных минимальных значений. Эти значения определяют пороги чувствительности для конкретных методов измерения, элементов и минералов. При содержаниях меньших этого порога находится зона нечувствительности, что отражается на виде сепарационной характеристике (рис. 5.9).
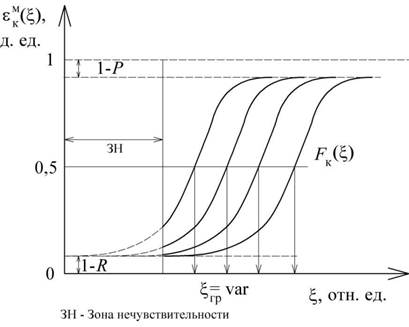
Рис. 5.9. Сепарационная характеристика при перестройке границы разделения
Граница разделения в информационных сепараторах, в зависимости от технологической задачи, свойств и состава сортируемого материала, от числа признаков разделения задаѐтся по-разному и на различных уровнях.
При единственном признаке разделения границей является абсцисса рабочей точки сепаратора при вероятности перехода частицы в концентрат или хвосты равной 0,5 (ордината рабочей точки равна 0,5). При двух независимых признаках разделения сепарационная характеристика представляет поверхность, а граница разделения – это проекция изолинии с ординатой 0,5 на поверхности сепарационной характеристики на горизонтальную плоскость. В случае трѐх разделительных признаков граница – это поверхность тела, внутри которого преобладают частицы одного вида (вероятность попадания их внутрь более 0,5), а снаружи – другого. При числе признаков разделения более трѐх граница – это гиперповерхность, которую целесообразно задавать многомерной функцией или в дискретном варианте координатами в n-мерном пространстве
(рис. 5.10).
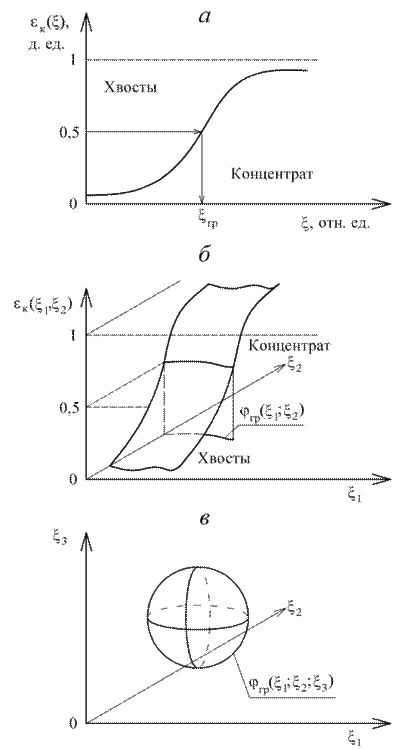
Рис. 5.10. Границы разделения информационного сепаратора при разном числе разделительных признаков:
а – одном; б – двух; в – трѐх (внутри тела концентрат, вне тела – хвосты)
Благодаря тому, что информационные методы включают вычислительные процедуры, становится возможным при измерении нескольких разделительных признаков комбинировать их, и разделение материала с многомерным фракционным составом осуществлять в одну операцию в одном аппарате. При этом может реализовываться разделение по специфической сепарационной
характеристике по границе произвольной формы (в n-мерном случае фракционного состава – это гиперповерхность n-ого порядка), которая может целенаправленно задаваться. На рис. 5.11 приведен пример границы разделения сепарационной характеристики для случая комбинирования двух признаков при разделении руды с одним полезным компонентом на два продукта.

Рис. 5.11. Сопоставление границ разделения при использовании информационного комбинированного метода и при сочетании двух различных прямых физико-механических методов в комбинированной схеме
Данная особенность информационных процессов разделения чрезвычайна важна. Благодаря ей, в одну операцию становится возможным разделение сырья, в прочих случаях обогащавшегося по комбинированным схемам с n операциями.
На рис. 5.12, приведены варианты границ разделения для двух случаев: первого – при использовании информационного комбинированного метода, в котором разделение по сложной границе θи (ξ1, ξ2) может осуществляться в одну операцию (рис. 5.12, а) и второго – сочетающего два прямых физико-механических метода разделения в комбинированной схеме, которая должна включать при показанном варианте кусочно-линейной аппроксимации сложной границы не менее шести операций (рис. 5.12, б). Данный пример иллюстрирует по одному потенциальному варианту принципиальных схем для каждого случая реализации границ, для случая (рис. 5.12, б) возможно несколько иных схем, отличающихся последовательностью выполнения операций. Принципиальные преимущества информационных методов перед другими в этом смысле неоспоримы.
Использование нескольких удаляющих органов или удаляющих органов на нескольких позициях не вызывает трудностей реализации в одну операцию многопродуктового разделения. Этот аргумент также указывает на
определенные преимущества использования информационных методов разделения для решения сложных технологических задач нестандартными методами.
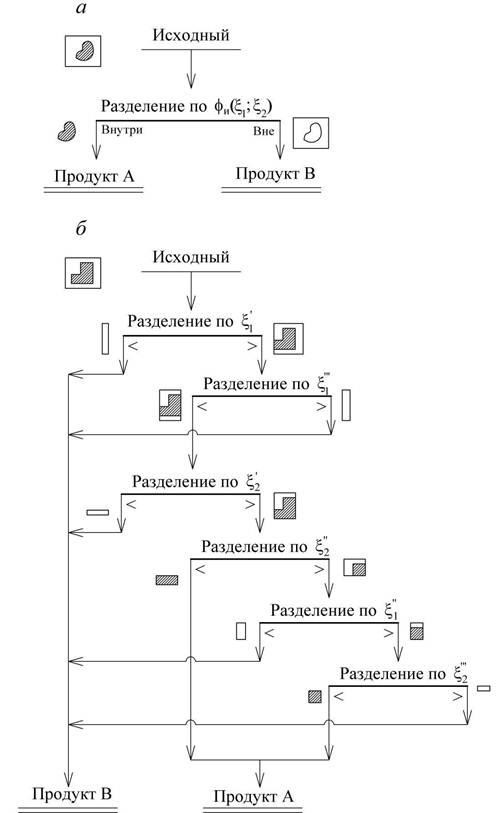
Рис. 5.12. Варианты принципиальных технологических схем при использовании информационного метода (а) и при сочетании двух различных прямых физико-механических методов при реализации разделения по сложной границе (б)
Для нескольких первичных или вновь полученных признаков в информационных методах для однократного разделения может быть задано нескольких границ для каждого из признаков.
Вычисленные содержания отдельных элементов αi дают возможность применять новые алгоритмы сортировки. Так, для каждого сортируемого куска можно рассчитать его относительную ценность (по отношению к массе куска):
∑
где ki – коэффициент, соответствующий цене металла на мировых рынках и учитывающий затраты на последующие обогащение и металлургию.
При сортировке с технологической задачей предварительной концентрации принятие решения об удалении в хвосты принимается по условию:
∑
По этому алгоритму, например, при вычисленных содержаниях элементов сульфидные медно-цинковые руды могут быть разделены на трѐхпродуктовом сепараторе на хвосты по вышеприведѐнному алгоритму, а также на медную и медно-цинковую руду, например, по дополнительному соотношению содержаний меди и цинка.
Такой подход может быть применѐн ко многим видам комплексных руд для решения аналогичных задач.
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Привести конкретный пример получения информации при бесконтактных воздействий на вещество и измерения свойств.
2. Каково соотношение физического свойства и признака разделения?
3. Привести примеры алгоритмов разделения частиц.
4. Какой из режимов информационных процессов разделения обеспечивает наиболее высокие технологические показатели?
5. Каковы особенности фракционных характеристик информационных методов разделения?
6. Какие погрешности разделения влияют на вид сепарационной характеристики информационного сепаратора?
ТЕМА 6
Дата добавления: 2014-12-23; просмотров: 534; Мы поможем в написании вашей работы!; Нарушение авторских прав |