ЛІНІЙНИХ АЛГЕБРАЇЧНИХ РІВНЯНЬ.

Розглянемо чисельні методи розв’язання систем лінійних алгебраїчних рівнянь

Ax=f (1)

де A - матриця m*m, x = ( x1, x2 , ... ,xm ) - шуканий вектор,

f =(f1, f2, ... , fm) -заданий вектор.

Припускаємо, що та визначник матриці А відмінний від нуля, так що існує єдиний розв’язок х. З курсу алгебри відомо, що систему (1) можна розв’язати за формулами Крамера*. Для великих m цей спосіб практично нереалізований тому, що потребує порядку m! aрифметичних дій. Тому широко використовуються інші методи розв’язання, наприклад, метод Гаусса**, який потребує дій.

Методи чисельного розв’язання системи (1) поділяються на дві групи:

-прямі методи;

-ітераційні методи.

У прямих (або точних) методах розв’язок x системи (1) відшукується за скінченну кількість арифметичних дій. Внаслідок похибок заокруглення прямі методи насправді не приводять до точного розв’язку системи (1) і назвати їх точними можливо лише залишаючи осторонь похибки заокруглення.

Ітераційні методи (їх також називають методами послідовних наближень) полягають у тому, що розв’язок x системи (1) відшукується як границя при 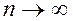послідовних наближень 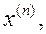де n- номер ітерації. Як правило, за скінченну кількість ітерацій ця границя не досягається.

МЕТОД ГАУСА.

Запишемо систему (1) у розгорнутому вигляді:

а11x1+a12x2+...+a1mxm=f1 ,

a21x1+a22x2+...+a2mxm =f2 , (2)

am1x1+am2x2+...+ammxm =fm .

Метод Гаусса розв’язання системи (2) полягає у послідовному вилученні невідомих x1, x2, ..., xm-1 з цієї системи.

Припустимо, що a11 0 . Поділив перше рівняння на a11, одержимо

x1+c12x2 +...+c1m xm =y1 , (3)

де : c1j=a1j /a11 ; j=2,m ; y1=f1/a11 .

Розглянемо тепер рівняння системи (2), що залишилися

ai1x1+ai2x2+...+aimxm=fi ; i= 2,m . (4)

Помножимо (3) на ai1 та віднімемо одержане рівняння з і-го рівняння системи (4), i=2,m.

У результаті одержимо наступну систему рівнянь:

x1+c12x2+...+c1jxj+...+c1mxm =y1 ,

(1) (1) (1) (1)

a22x2+... +a2jxj+...+a2mxm=f2 ,

............................................ (5)

(1) (1) (1) (1)

am2x2+...+amjxj+...+ammxm=fm .

Tут позначено:

(1) (1)

aij=aij-c1jai1; fi=fi -y1ai1; i,j=2,m . (6)

Матриці такої стуктури заведено позначати так:

У системі (5) невідоме х міститься тільки в першому рівнянні, тому у подальшому достатньо мати справу із скороченою системою рівнянь:

(1) (1) (1) (1)

a22x2 +...+a2jxj +...+a2mxm =f2 ,

.............................................. (7)

(1) (1) (1) (1)

am2x2 +...+amjxj +...+ammxm =fm .

Тим самим ми здійснили перший крок методу Гаусса . Коли 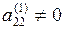, то з системи (7) зовсім аналогічно можна вилучити невідоме x2 і прийти до системи, еквівалентній (2),що має матрицю такої структури:

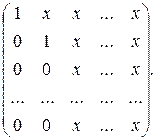
При цьому перше рівняння системи (5) залишається без зміни.

Вилучаємо таким же чином невідомі х 3, х4 ,... ,x m-1 , приходимо остаточно до системи рівнянь виду:

x1 +c12x2 +...+c1,m-1xm-1+c1mxm =y1,

x2 +...+c2,m-1xm-1+c2mxm =y2 ,

xm-1+cm-1,mxm=ym-1,

xm=ym ,

що еквівалентна початковій системі (2) .

Матриця цієї системи

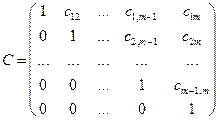
містить нулі усюди нижче головної діагоналі. Матриці такого виду називаються верхніми трикутними матрицями. Нижньою трикутною матрицею називається така матриця, у якої дорівнюють нулю усі елементи, що містяться вище головної діагоналі.

Побудова системи (8) складає прямий хід методу Гаусса. Зворотний хід полягає у відшуканні невідомих х1, ... ,хm з системи (8). Тому що матриця системи має трикутний вигляд, можна послідовно, починаючи з хm, відшукати всі невідомі. Дійсно, xm=ym,

x m-1 =ym-1 -cm-1,m x m i т. д.

Загальні форми зворотного ходу мають вигляд:

m

xi =yi - å cijxj ; i=m-1,1; xm =ym . (10)

j=i+1

При реалізації на ПК прямого ходу методу Гаусса немає необхідності діяти із змінними x1 ,x2 ,... ,xm. Досить вказати алгоритм, за яким початкова матриця А перетворюється до трикутного вигляду (9), та вказати відповідне перетворення правих частин системи.

Одержимо ці загальні формули.

Нехай вже здійснені перші к-1 кроків, тобто вже вилучені змінні

x1 , x2,..., xk-1 .

Тоді маємо систему:

x1+c12 x2 +...+c1,k-1xk-1+ c1kxk+....+c1mxm =y1 ,

x2 +...+c2,k-1xk-1+ c2kxk+....+c2mxm =y2 ,

..............................................

xk-1+ck-1,kxk+...+ck-1,mxm=yk-1 , (11)

(k-1) (k-1) (k-1)

akkxk+...+akmxm =fk ,

(k-1) (k-1) (k-1)

amkxk+...+ammxm =fm .

Розглянемо К-те рівняння цієї системи:

(k-1) (k-1) (k-1)

akkxk+...+akmxm=fk ,

та припустимо, що . Поділивши обидві частини цього рівняння на , одержимо

xk+ck,k+1xk+1+...+ckmxm=yk , (12)

(k-1) (k-1) (k-1) (k-1)

де ckj=akj / akk ; j=k+1,m ; yk=fk / akk .

Далі помножимо рівняння (12) на та віднімемо одержане співвідношення з i-го рівняння системи (11). У результаті остання група рівнянь системи (11) набуває наступного вигляду:

x k+ck,k+1xk+1 +...+ ckmxm=yk,

(k) (k) (k)

ak+1,k+1xk+1+...+ ak+1,mxm=fk+1,

.......................................

(k) (k) (k)

am,k+1xk+1+... + ammxm=fm ,

(k) (k-1) (k-1) (k) (k-1) (k-1)

де: aij =aij - aikckj ; i,j=k+1,m ; fi= fi - aikyk ; i=k+1,m .

Таким чином, у прямому ході методу Гауса коефіцієнти рівнянь перетворюються за наступним правилом

(0)

akj =akj ; k,j=1,m ;

(k-1) (k-1)

ckj=akj /akk ; j=k+1,m ; k=1,m ; (13)

(k) (k-1) (k-1)

aij =aij - aikckj ; i,j=k+1,m ; k=1,m . (14)

Обчислення правих частин системи (8) здійснюється за формулами:

(0) (k-1) (k-1)

fk=fk ; yk = fk / akk ; k=1,m ; (15)

(k) (k-1) (k-1)

fi = fi - aikyk ; k=1,m . (16)

Коефіціенти cij і праві частини yi ; i=1,m ; j=i+1,m зберігаються у пам’яті ЕОМ і використовуються при здійсненні зворотнього ходу за формулами (10).

Основним обмеженням методу є припущення, що усі елементи 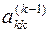, на які здійснюється ділення, відрізняються від нуля. Число 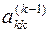називається провідним елементом на К-му кроці вилучення. Навіть, якщо деякий провідний елемент не дорівнює нулеві, а просто є близьким до нуля, в процесі обчислень може мати місце нагромадження похибок. Вихід з цієї ситуації полягає в тому, шо як провідний елемент вибирається не , а інше число ( тобто на К-му кроці вилучається не xk, а інша змінна xj , ) . Така стратегія вибору провідних елементів здійснюється в методі Гаусса з вибором головного елементу, який буде розглянуто пізніш.

А тепер підрахуємо число арифметичних дій, що необхідні для розв’язання системи за допомогою методу Гаусса. Оскільки виконання операцій множення і ділення на ПК потребує набагато більше часу, ніж виконання додавання і віднімання, обмежимось підрахуванням числа множень і ділень.

1.Обчислення коефіцієнтів 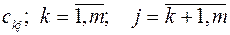за формулами (13) потребує:

(m-k)=1+2+...+(m-1)= ділень .

2.Обчислення усіх коефіцієнтів за формулами (14) потребує

Множень. Тут ми використовуємо за індукцією рівність ),

яку легко перевірити. Таким чином, обчислення ненульових елементів трикутної матриці С потребує

операцій множення і ділення.

3.Обчислення правих частин yk за формулами (15) потребує m

ділень, а відшукання за формулами (16)

множень. Разом, обчислення правих частин перетвореної системи (8) потребує m + m(m-1)/2= m(m+1) дій множення і ділення.

Усього для реалізації прямого ходу методу Гаусса необхідно виконати

дій.

4. Для реалізації зворотнього ходу методу Гауса за формулами (10) необхідно

множень.

Всього, для реалізації методу Гаусса необхідно виконати

дій множення і ділення, причому основний час витрачається на прямий хід. Для великих m число дій множення і ділення у методі Гаусса близьке до За витратами часу та необхідній машинній пам’яті метод Гаусса придатний для розв’язання систем рівнянь (2) загального вигляду з кількістю змінних m порядку 100.