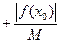Лекція 2

3.2 Метод пропорційних частин (хорд)

Потрібно знайти корінь рівняння f(x) на відрізку [а, b]. Відомо, що f(x) неперервна на [а, b]. і f(a)*f(b)<0; крім того, f((x ) і f(((x ) на відрізку [а, b]. зберігають свій знак. Для розв’язання рівняння використаємо метод пропорційних частин (метод хорд), який дає розв’язання задачі для досить малих 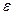швидше, ніж попередній метод.

Для наближеного кореня рівняння (1) замінюємо функцію f(x) на відрізку [а, b].лінійною функцією, яка на кінцях відрізку [а, b].приймає ті ж самі значення, що і функція f(x).

P(x)= f(a) + (x-a)(f(b)-f(a))/(b-a)

В якості наближеного значення кореня f(x) беремо корінь функції P(x), тобто знаходимо таке значення x₁, при якому P(x₁)=0. Це значення (перше наближення) визначається по формулі

x₁ = a - f(x)(b-a)/ )(f(b)-f(a)) (2)

Далі розглянемо відрізки [a, x], [x, b] і виберемо з них той, на кінцях якого функція f(x) має протилежні знаки. Ті ж обчислення виконуємо на вибраному відрізку і отримуємо друге наближення кореня x₂ і т.д., поки не отримаємо корінь рівняння (1) із заданою похибкою.

Обчислювальна схема методу пропорційних частин реалізовується так.

До початку ітераційного процесу задаємо точність e, з якою треба отримати розв’язання, потім:

а) приймаємо xl = a; та xr = b;

б) на кожному кроці ітераційного процесу обчислюємо наближення до кореня по формулі:

x=( xlf(x)- xr f(xr))/( f xr)- f(xl)) (3)

в) перевіряємо виконання нерівності

çf (х)ç< e. (4)

і якщо нерівність (4) виконується, то x вважаємо розв’язанням рівняння (1), а інакше продовжуємо обчислення;

г) перевіряємо умову f (х)× (f(xl) > 0, і при виконанні цієї умови приймаємо xl = x, а інакше xr = x, та повторюємо обчислення з пункту б).

Дамо геометричну інтерпретацію методу. Нехай функція f(x) має графік. На кінцях відрізка функція f(x) приймає значення різних знаків. З'єднаємо точки (a, f(a)) та (b, f(b)) прямою, і точку перетину цієї прямої з віссю X приймемо за перше наближення до кореня. Цей процес продовжуємо доти, поки не виконається умова закінчення обчислень.

Структурна схема алгоритму відрізняється від структурної схеми попереднього методу лише способом обчислення поточної змінної x..

3.3 Метод Рибакова

Необхідно знайти декілька дійсних коренів рівняння (1).на відрізку [a, b], причому похідна функція f’(x) на [a, b] може мати розриви першого роду.

Для розв’язання цієї задачі доцільно використати метод Рибакова. Опишемо обчислювальну схему цього методу. До початку ітераційного процесу задаємо точність e, з якою потрібно отримати корені рівняння (1), і виберемо деяке число m, при умові, що max çf^¢(х)ç< m.

Завищення m не порушує збіжності методу, а тільки сповільнює.

Потім: 1)вважаємо x₀ = a;

2)для кожного k = 1,2… ( k - номер ітерації):

обчислюємо наближення до кореня по формулі:

x_k+1 = x_k + çf (х) ç/m;

- перевіряємо умову x_k+1 < b,

і, якщо умова не виконується, то вважаємо, що всі корені знайдені, інакше продовжуємо обчислення;

- перевіряємо виконання умови çx_k+1 - x_k,ç> e, і якщо вона виконується, то повторюємо обчислення з новим k; а інакше вважаємо x_k+1 одним із коренів рівняння і продовжуємо обчислення;

3) обчислюємо початкове наближення до наступного кореня по формулі x₀ = x_k+1+e і переходимо до п.2)

Дамо геометричну інтерпретацію розглянутого ітераційного процесу. На мал.5 зобразимо функцію y=çf (х)ç. Задано початкове наближення до кореня x₀=a. Через точку (a, f(a)) проводимо пряму (тангенс кута нахилу рівний m), точку перетину цієї прямої віссю X приймаємо за перше наближення до першого кореня. Через точку (x₁, f(x₁)) проводимо пряму, паралельну першій.

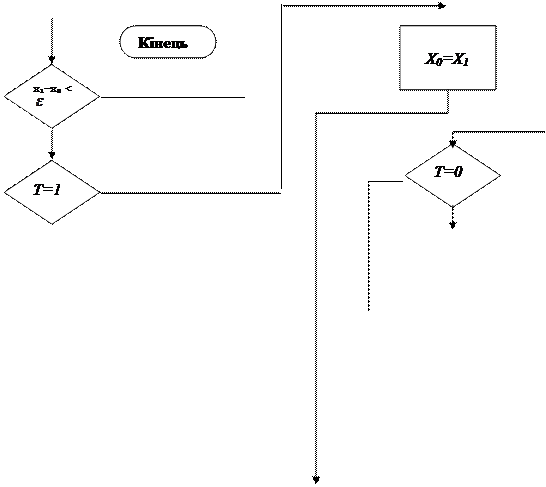
Блок-схема алгоритму метода Рибакова:

	X1=X0+

Точку перетину цією прямою з віссю X приймаємо за друге наближення до першого кореня і т.д., поки не отримаємо корінь. Відступивши від отриманого праворуч на e, приступаємо до знаходження наступного кореня.

Тут змінна T (прапорець) приймає значення 1 після першого виконання умови çx_k+-x_k,ç£e,. При цьому допоміжні змінні xl та xr запам'ятовують значення x_k+1. Значення x=( xl + xr)/2 буде надруковано, якщо при новому значенні x_k+1 не виконується вказана раніше умова. Інакше знову змінюється допоміжна змінна xr (набуває нового значення x_k+1), а xl зберігає своє значення і знову обчислюється нове значення x_k+1.