КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Метод Ньютона (дотичних)
Метод Ньютона дуже широко використовується при побудові ітераційних алгоритмів. Його популярність пояснюється тим, що, для визначення інтервалу, в якому міститься корінь, не потрібно знаходити значення функції з протилежними знаками. Замість інтерполяції (наближення) по двом значенням функції в методі Ньютона здійснюється екстраполяція за допомогою дотичної до кривої в даній точці.
Нехай корінь рівняння f(х)=0 відділений на відрізку [a, b], причому f'(х) і f"(х) неперервні і зберігають постійні знаки на всьому відрізку [а, b].
Геометричний зміст методу Ньютона полягає в тому, що дуга кривої у=f(х) замінюється дотичною до цієї кривої (звідси і друга назва: метод дотичних).
Перший випадок. Нехай f(а)<0, f(b)>0, f'(х)>0, f'(x)>0 (мал.5а), або f(а)>0, f(b)<0, f'(х)<0, f”(х)<0 (мал.5б). Проведемо дотичну до кривої у=f(х) у точці B0(b; f(b)) і знайдемо абсцису точки перетину дотичної з віссю Ox.
Відомо, що рівняння дотичної в точці B0(b; f(b)) має вигляд:
y – f(b) = f¢(b)×(x-b)
Вважаючи y=0, x=x1, отримаємо
x1 = b - f(b)/f¢(b) (5)
Тепер корінь рівняння знаходиться на відрізку [a, x1]. Застосовуючи знову метод Ньютона, проведемо дотичну до кривої в точці В1(x1; f(х1)) і отримаємо
x2 = x1 - f(х1)/ f¢(х1)
І взагалі
xn+1 = xn - f(хn)/ f¢(хn) (6)
Одержуємо послідовність близьких значень x1, x2,..., xn кожний наступний член якої ближче до кореня 
, ніж попередній. Однак всі xn залишаються більше істинного кореня , тобто xn - наближене значення кореня xn з надлишком.
Другий випадок. Нехай f(а)<0, f(b)>0, f'(х)>0, f”(х)<0 (мал.6а) або f(а)>0, f(b)<0, f'(х)<0, f”(х)>0 (мал.6б).
Якщо знову провести дотичну до кривої у=f(x) в точці В, то вона перетне вісь абсцис у точці, що не належить відрізку [a, b]. Тому проведемо дотичну в точці A0(a; f(a)) і запишемо її рівняння для даного випадку:
y – f(a) = f¢(a)(x-a)
Вважаючи у=0, x=x1, знаходимо
x1 =a- f(a)/ f¢(a) (7)
Корінь знаходиться тепер на відрізку[x1, b]. Застосовуючи знову метод Ньютона, проведемо дотичну в точці A1 (x1; f(x1)) і отримаємо
x2 =a- f(x1)/ f¢( x1)
Мал.6
І взагалі
xn+1 =a- f(xn)/ f¢( xn) (8)
Одержуємо послідовність близьких значень х1, х2,..., xn кожний наступний член якої ближче до істинного кореня , ніж попередній, тобто xn — близьке значення кореня з недоліком.
Порівнюючи ці формули з раніше виведеними, помічаємо, що вони відрізняються друг від друга тільки вибором початкового наближення: у першому випадку за x0 приймався кінець b відрізка, в другому — кінець a.
При виборі початкового наближення кореня необхідно керуватися наступним правилом: за вхідну точку слідує вибирати той кінець відрізка [а, b], на якому знак функції співпадає зі знаком другої похідної. У першому випадку f(b)•f”(х)>0 і початкова точка b=x0, в другому f(a)•f”(x)>0 і в якості початкового наближення беремо а=x0.
Для оцінки похибки можна користуватися загальною формулою
çx - xnç£çf (хn)ç/m, (9)
де m = minçf¢ (х)ç [а £ x £ b].
Ця формула годиться і для методу хорд. У випадку, коли відрізок [а, b] настільки малий , що наньому виконується умова
m2<2m1, де m2 = maxçf¢¢ (х)ç, a m1 = minçf¢ (х)ç [а £ x £ b].
Точність наближення на k-ому кроку оцінюється так:
якщо çxk+1 - xk ç<e, , то çx - xk ç<e2.
Якщо похідна f'(x) мало змінюється на відрізку [а, b], то для спрощення обчислень можна користуватися формулою
xn+1 = xn - f(xn)/ f¢( xn) (10)
тобто значення похідної в початковій точці достатньо обчислити тільки один раз. Геометрично це означає, що дотичні в точках Вn(xn; f(xn)) замінюються прямими, паралельними до дотичної, проведеної до кривої у=f(х) в точці В0(x0; f(x0)) (мал.7).
Приклад. Методом дотичних уточнити до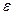 
=0.001 корінь рівняння x3+Зx2-3=0, розташований на відрізку [-2.75; -2.5].
Розв’язання. Раніше було встановлено, що f(-2.75)•f"(х)>0. Тому, щоб скористуватися методом дотичних, слід вибрати x0=-2.75. Обчислення будемо вести по формулі (10). Знаходимо f'(x0)=Зх2+6x; f'(x0)=f'(- 2.75)=6,1875.
Для зручності всі обчислення зведемо в наступну таблицю:
Таблиця 1
| N | xп | x3п | x2п | 3x2п | f(xп) | -f(xn)/6,1875 |
| -2,75 -2,571 -2,545 -2,537 -2,534 -2,533 | -20,797 -16,994 -16,484 -16,329 -16,271 | 7,5625 6,6100 6,4770 6,4364 6,4212 | 22,6875 19,8300 19,431 19,309 19,2636 | -1,111 -0,164 -0,053 0,020 0,007 | 0,179 0,026 0,008 0,003 0,001 |
З таблиці 1 видно, що çx5 - x4 ç<0.001, тому x = x5 =-2.533.
Дата добавления: 2014-12-23; просмотров: 243; Мы поможем в написании вашей работы!; Нарушение авторских прав |