Метод половинного ділення.

Цей метод використовується, якщо відомо, що f(x) неперервна на відрізку [а, b] та f(а)×f(b)<0.

Основна ідея методу. Ділимо відрізок [а, b], на якому шукаємо корінь рівняння, навпіл і, якщо çf((а+b)/2)ç > вибираємо той із відрізків [a,(a+b)/2] чи [(a+b)/2, b], на кінцях якого f(x) має різні знаки. Цей відрізок знову ділимо навпіл та повторюємо ті ж дії поки не отримаємо корінь із заданою точністю.

Метод половинного ділення зручно застосовувати для приблизного знаходження кореня даного рівняння, бо із збільшенням точності зростає об’єм виконаної роботи через повільну збіжність ітераційного процесу.

Опишемо обчислювальну схему методу. До початку обчислення задаємо число e- точність, з якою потрібно отримати корінь рівняння. Потім:

а) приймаємо xl = a; та xr = b;

б) на кожному кроці процесу обчислюємо x = (xl+xr)/2, y = f(x); і

в) перевіряємо нерівність çf (х)ç < e і, при виконанні умови вважаємо x коренем рівняння; а в протилежному випадку перевіряємо умову f (х)(f(xl)>0, і при виконанні цієї умови приймаємо xl = x, а інакше xr = x, та повторюємо обчислення пункту б).

Дамо геометричну інтерпретацію цього методу. Нехай функція f(x) має графік, зображений на мал.2. При обчисленні значення (a+b)/2 знаходимо середину відрізка [а, b]. Обчислення величини f((a+b)/2) означає проведення перпендикуляра із точки (a+b)/2 до перетину з графіком функції f(x).

Якщо çf (х_k)ç> e, то для продовження обчислювального процесу залишаємо той відрізок, на кінцях якого f(x) має різні знаки. У даному випадку цей відрізок [(a+b)/2, b]. На цьому крок ітераційного процесу закінчується. Повторюємо ітерації поки не буде виконана умова закінчення обчислень.

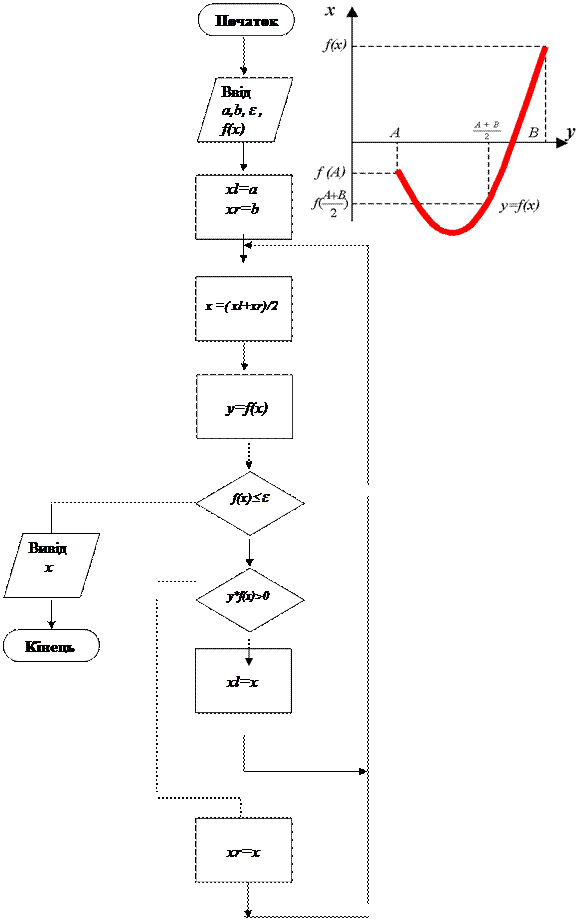
Наведемо структурну схему алгоритму методу половинного ділення:

Структурна схема алгоритму методу половинного ділення: