Определение рабочей точки центробежного насоса

Для решения задачи необходимо :

1. Составить уравнение гидравлической сети.

2. Построить графическое изображение этого уравнения в координатах Q- H.

3. Нанести на этот график характеристику насоса и определить координаты точки пересечения напорной характеристики насоса и характеристики сети (координаты рабочей точки).

Последовательность решения задачи.

1). Выбираем два сечения - н-н и к-к, перпендикулярные направлению

движения жидкости и ограничивающие поток жидкости (Рис. 1).

Сечение н-н проходит по свободной поверхности жидкости в резервуаре 2, а сечение к-к – под поршнем в цилиндре 3.

2). Применяем в общем виде закон сохранения энергии для сечений н-н и к-к с учетом того, что жидкости добавляется энергия в насосе, равная потребному в данной сети напору H_потр:

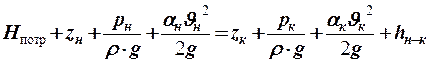
(26)

3). Раскрываем содержание слагаемых уравнения (26) для нашей задачи.

Для определения величин z_н и z_к выбираем горизонтальную плоскость сравнения 0-0. Для удобства ее обычно проводят через центр тяжести одного из сечений. В нашем случае плоскость 0-0 совпадает с сечением н-н.

z_н и z_к- вертикальные отметки центров тяжести сечений. Еслисечение расположеновыше плоскости 0-0, отметка берется со знаком плюс, если ниже- со знакомминус.

z_н=0; z_k=H₁+H₂.

р_н, р_к - абсолютные давления в центрах тяжести сечений.

Давление на поверхности открытых резервуаров равно атмосферному, а взакрытых резервуарахилив трубе - сумме атмосферного давления и показания прибора (манометрическое давление берется со знакомплюс, вакуумметрическое - со знаком минус). Вакуумметрическое давление – это отрицательное манометрическое.

р_н = р_ат+ р_м ;

р_{к =} R/S + р_{ат .}, где S=p×D²/4 – площадь сечения поршня.

J_н , J_к - средние скорости движения жидкости в сечениях.

Согласно закону сохранения количества вещества через любое сечение потокапроходитодин и тот же расход жидкости:

Здесь Q₁ и Q₂ - расходы в сечениях всасывающего и напорного трубопроводов. Учитывая, что Q =J×w, вместо (27) получим:

где w_н, w₁, w₂, w_к - площади соответствующих сечений.

Поскольку площади сечений резервуаров значительно больше площадей сечений труб, скорость J_н очень мала по сравнению со скоростями в трубах J₁ и J₂ и величиной a_нJ_н²/2gможно пренебречь. Скорость J_к= Q/w_к.

a_н и a_к - коэффициенты Кориолиса ; a= 2 при ламинарном режиме движения, a=1 при турбулентном режиме.

Принимаем: J_н » 0; J_к= Q/w_к==Q/(p×D²/4).

Потери напора h_н-к при движении жидкости от сечения н-н к сечению к-к складываются из потерь во всасывающем и нагнетательном трубопроводах, причем в каждом трубопроводе потери разделяются на потери по длине и местные:

	hн-к= h1 + h2= hдл.1 + hф + hпов.1 +hдл.2 + hкр. +2hпов.+ hвых.	(29)
	- потери по длине на всасывающем трубопроводе.
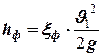
	- потери в приемной коробке (фильтре). xф зависит от диаметра всасывающего трубопровода (при d=140мм xф = 6,2, приложение 5).
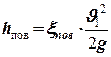
	- потери на поворот во всасывающем трубопроводе, xпов. - коэффициент сопротивления при резком повороте на угол 90° (xпов =1,32 - приложение 5).
	- потери по длине на нагнетательном трубопроводе.
	xкр. =0 - задается по условию.
	- потери на поворот в нагнетательном трубопроводе, xпов. - коэффициент сопротивления при резком повороте на угол 90°(xпов =1,32 - приложение 5).
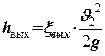
	- потери при выходе из трубы в резервуар (xвых =1 - приложение 5).

Для определения коэффициентов местных сопротивлений переходим по гиперссылке в справочный файл Приложение.doc (делаем щелчок мышью по слову приложение).

С учетом вышеприведенных зависимостей, вместо (29) можно записать:

(30)

4). Подставляем в уравнение (26) определенные выше значения слагаемых:

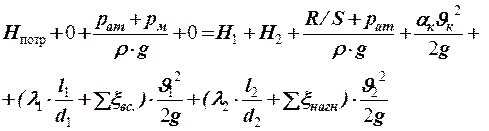; В этом уравнении атмосферное давление сокращается, рм, R, hвс, hн, dвс, dн, lвс, lн известны по условию; åxвс = xвх+xпов.=6,2+1,32=7,54; åxнагн. = xкр+2xпов+xвых..=0+2×1,32+1=3,64.

(31)

5). Выражаем в уравнении (31) скорости J₁ и J₂ через расход жидкости:

J1 = Q / w1=4Q/p×d12; J2 = Q / w2=4Q/p×d22;

6). Упрощаем уравнение (31) и определяем потребный напор H_потр. :

(32)

Зависимость (32) и представляет собой уравнение (характеристику) гидравлической сети. Это уравнение показывает, что в данной сети напор насоса расходуется на подъем жидкости на высоту (H₁ +H₂), на преодоление противодавления R/S - р_м и на преодоление гидравлических сопротивлений.

7. Строим характеристику насоса Д-320 и наносим на нее графическое изображение характеристики сети (32).

Для построения характеристики сети задаемся несколькими значениями расхода жидкости из рабочего диапазона насоса Д-320 и вычисляем по уравнению (32) значение потребного напора H_потр. Перед вычислением определяем при температуре t = 30°С плотность и вязкость жидкости по справочным данным.

Плотность жидкости при другой температуре можно определить по формуле:

r_t = r₀ / (1+a×Dt),

где r_t - плотность жидкости при температуре t=t₀ +Dt;

Dt - изменение температуры;

t₀ - температура, при которой плотность жидкости равна r₀;

a - коэффициент температурного расширения (в среднем для минеральных

масел и нефти можно принять a=0,0007 1/° C, для воды, бензина, керосина

a=0,0003 1/° C) .

2. Вязкость при любой температуре определяется по формуле:

n_t = n₂₀×e^b×(t-20);b = 1/(t₂ - t₁)× ln (n_t2/n_t1). - приложение 3

t₀=20°, t=30°, Dt=30-20=10, r₀=884, a=0,0007 1/° C, n₂₀=0,25см²/c, t₁=20°, t₂=40°, n_t1=0,25см²/c, n_t2=0,15см²/c. Все вычисления будут производиться в Excel.

Анализ формулы (32) показывает, что при задании расхода Q все величины в правой части уравнения известны, кроме коэффициента трения l.

Последовательность вычисления l:

	Re < 2300	l=64 / Re
	Re > 2300	l = 0,11×(68/Re + Dэ/d)0,25

Принимаем величину абсолютной шероховатости трубопровода

D_э = 0,5 мм (трубы стальные, сварные, бывшие в употреблении, приложение 4). Вычисления и построение графиков выполняем на ЭВМ с помощью электронных таблиц (Microsoft Excel).

N_дв.=r×g×H×Q/h=878×9,8×59×76×10^-3/0,68=56,7 кВт.

ПРИЛОЖЕНИЯ

Приложение 1