
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Нахождение числовых характеристик выборки
Среднее значение выборки вычисляется по формуле
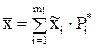 , (4)
, (4)
где 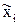 – середины уточненных интервалов (табл. 2, гр. 7),
– середины уточненных интервалов (табл. 2, гр. 7),  – частоты попадания в
– частоты попадания в 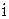 -й интервал (гр. 6). Промежуточные результаты
-й интервал (гр. 6). Промежуточные результаты 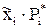 можно поместить в
можно поместить в
графу 9.
Выборочная дисперсия вычисляется по формуле
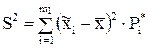 (5)
(5)
или 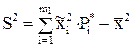 . (6)
. (6)
Промежуточные значения  можно поместить в графу 10.
можно поместить в графу 10.
Выборочные коэффициенты асимметрии и эксцессвычисляются по формулам
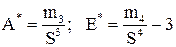 , (7)
, (7)
где 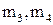 – выборочные центральные моменты 3 и 4-го порядка соответственно:
– выборочные центральные моменты 3 и 4-го порядка соответственно:
 (8)
(8)
или 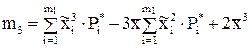 , (9)
, (9)
 (10)
(10)
Промежуточные значения  можно поместить в графы 11 и 12.
можно поместить в графы 11 и 12.
Замечание. Более точными будут выборочные характеристики, полученные по всей выборке. Например,
 (11)
(11)
Аналогично вычисляются значения 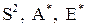 .
.
Выборочная медиана 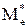 может быть определена по всей упорядоченной вы-
может быть определена по всей упорядоченной вы-
борке следующим образом: если объем выборки n - нечетное число, то
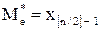 ; (12)
; (12)
если n четное, то 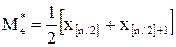 , (13)
, (13)
где 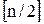 - целая часть
- целая часть  .
.
Для выборки из генеральной совокупности значений непрерывной случайной величины выборочная медиана может быть определена по графику эмпирической функции распределения как абсцисса точки с ординатой 1/2.
Найденные числовые характеристики выборки могут служить оценками соответствующих характеристик генеральной совокупности.
Дата добавления: 2014-12-23; просмотров: 279; Мы поможем в написании вашей работы!; Нарушение авторских прав |