Пример выполнения и оформления лабораторной работы. Дана выборка, содержащая двести элементов (табл.1)

Дана выборка, содержащая двести элементов (табл.1). Упорядочим выборку. Наименьшее число равно 0,000 994, наибольшее 3,666 642. Интервал (0,000; 3,700)

разделим на 20 равных частей. Границы интервалов занесем в графу 2 таблицы 2.

Число элементов, попавших в 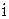–й интервал, занесем в графу 3. Два числа - 3,014 916, 3,666 642, резко отличающиеся от других и полученные, видимо, за счет грубых ошибок опыта, можно отбросить. Таким образом, .

Объединим интервалы так, чтобы новые интервалы содержали не менее 8-10 элементов. Новые границы интервалов, а также число элементов, попавших в уточненные интервалы, поместим в графы 4 и 5. В графу 6 поместим частоты попаданий в каждый интервал. Далее таблица 2 заполняется в соответствии с описанием работы.

По полученным данным строится график эмпирической функции распределения (рис.1) и гистограмма (рис.2).

По формулам (4), (6), (7) вычисляются выборочные среднее, дисперсия, коэффициент асимметрии и эксцесс.

Предварительно удобно вычислить следующие суммы:

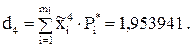
Тогда .

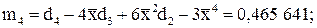
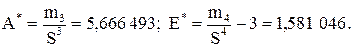
Выборочную медиану 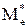определим по графику эмпирической функции рас-

пределения: .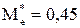

Контрольные вопросы

1. Разъясните понятия: генеральная совокупность, случайная выборка, оценка.

2. Что такое эмпирическая функция распределения и как она вычисляется по данным выборки ?

3. Что такое гистограмма распределения и как она строится по данным

выборки ?

4. Какие оценки параметров называются точечными ?

5. Что такое состоятельность, эффективность и несмещенность точечных оценок?

6. В чем состоит метод моментов определения точечных оценок ?