Определение оценок параметров распределения

После выдвижения гипотезы о виде закона распределения определяем по группированной выборке оценки параметров распределения.

Например, для нормального закона требуется найти оценки математического ожидания и среднего квадратичного отклонения; для показательного закона –оценку параметра . Для большинства законов параметры либо являются математическим ожиданием и дисперсией, либо являются функциями этих числовых характеристик. Поэтому в подавляющем числе случаев для определения оценок параметров распределения достаточно определить оценки математического ожидания и дисперсии.

Оценки математического ожидания и дисперсии определяются по формулам

; (1)

, (2)

где 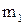– число уточненных интервалов, 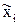– середины уточненных интервалов;

– частоты попадания в 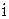-й интервал.

Замечание. Оценки параметров выборки, определенные по негруппированной выборке, будут более точными, но громоздкость вычислений не всегда оправдывается улучшением результата. При использовании ЭВМ оценки параметров рекомендуется определять по всей выборке.