Пример выполнения и оформления лабораторной работы

Дана выборка, содержащая 200 элементов (см. лаб. раб. 1, табл. 1). Упорядочим выборку. Наименьшее число равно 0,000 9 94, наибольшее число равно

3,666 642. Интервал (0,0001; 3,700) разделим на 20 равных частей. Границы интервалов занесем в графу 2 таблицы 1. Число элементов, попавших в i-й интервал, занесем в графу 3. Два числа - 3,014 916, 3,666 642, резко отличающиеся от других и полученные, видимо, за счет грубых ошибок опыта, можно отбросить. Таким образом, . Объединим интервалы таким образом, чтобы новые интервалы содержали не менее 8-10 элементов. Новые границы интервалов, а также число элементов, попавших в уточненные интервалы, поместим в графы 4 и 5, в графу 6 поместим частоты попаданий в каждый интервал. По полученным данным построим гистограмму (см. лаб. раб. 1, рис.2,). Вид гистограммы дает право выдвинуть гипотезу о показательном распределении генеральной совокупности.

Оценку параметра показательного закона можно определить следующим обра-

зом: 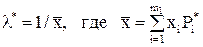. - число уточненных интервалов.

Для удобства значения поместим в графу 8, значения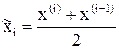

предварительно были помещены в графу 7. Оценка математического ожидания 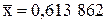, оценка параметра показательного закона . Для вычисления величины - меры расхождения теоретического и статистического распределений - вычислим теоретические вероятности попаданий значений случайной величины в 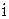– й интервал по формуле (6). Значения для каждого 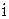занесем в графу 11. Вычисленное значение .

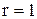В данном примере по выборке определен один параметр . Следовательно, и число степеней свободы распределения 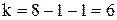. Зададимся уровнем значимости 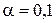. По таблице А2 находим . Вычисленное значение меньше , следовательно, гипотеза не отвергается с уровнем значимости .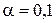

Контрольные вопросы

1. Что такое эмпирическая функция распределения, как она вычисляется по данным выборки?

2. Что такое гистограмма распределения, как она строится по данным выборки?

3. Объяснить содержательный смысл критерия как меры близости эмпирического и теоретического распределений.

4. Как учитывается при пользовании критерием согласия факт определения

параметров теоретического распределения по данным выборки?

5. Почему при гипотезу следует отбросить?

Таблица 1

№ п/п	J (до объединения)	(до объеди-не-ния)	J (после объединения)	(после объ-един-ения)
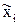
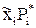
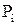
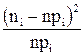
	(0,000-0,185)		(0,000-0,185)		0,252 525	0,0925	0,233 585		0,244 485	0,052 3541
	(0,185-0,370)		(0,185-0,370)		0,191 919	0,2775	0,053 2575		0,184 713	0,055 6801
	(0,370-0,555)		(0,370-0,555)		0,141 414	0,4625	0,065 4039		0,139 554	0,004 9092
	(0,555-0,740)		(0,555-0,740)		0,111 111	0,6475	0,071 9444		0,105 434	0,060 525
	(0,740-0,925)		(0,740-0,925)		0,085 859	0,8325	0,071 4778		0,079 657	0,095 5973
	(0,925-1,110)		(0,925-1,295)		0,101 010	1,11	0,112 1211		0,105 650	0,040 3464
7	(1,110-1,295)
	(1,295-1,480)
	(1,480-1,665)		(1,295-1,850)		0,070707	1,5725	0,111 1867		0,079 914	0,210 0245
	(1,665-1,850)
	(1,850-2,035)
	(2,035-2,220)
	(2,220-2,405)		(1,850-2,775)		0,045454	2,3125	0,105 1123		0,045 678	0,000 2145
	(2,405-2,590)
	(2,590-2,775)	1
	(2,775-2,960)
	(2,960-3,145)
	(3,145-3,330)
	(3,330-3,515)
	(3,515-3,700)