КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Пример выполнения и оформления лабораторной работы. Дана выборка объемом (табл
Дана выборка объемом 
(табл. 1) из нормальной генеральной совокупности.
Таблица 1
| № п/п | Элементы выборки | № п/п | Элементы выборки | № п/п | Элементы выборки | № п/п | Элементы выборки |
| 0,047 | 0,496 | -1,7888 | 0,118 | ||||
| - 0,451 | - 0,748 | - 0,855 | 0,242 | ||||
| 1,661 | - 0,083 | 0,095 | 1,739 | ||||
| 1,290 | - 0,312 | 1,192 | - 0,412 | ||||
| 0,380 | -1,372 | - 0,059 | - 0,426 |
Найдем по формулам (1) и (3) оценки математического ожидания и дисперсии, 
;
; 
.
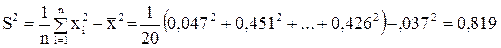Так как объем выборки невелик, для построения доверительного интервала для математического ожидания воспользуемся формулой (8):
.
Доверительную вероятность 
положим равной 0,95, . По таблице А3 по заданным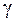 
и 
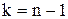определим 
.
Доверительный интервал для математического ожидания, соответствующий доверительной вероятност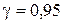и 
:
или 
.
При построении доверительного интервала дисперсии положим 
. Тогда 
. 
определим из условия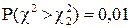 
; 
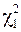определим из условия 
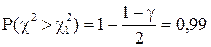(рис. 1).
По таблице А2 по заданным вероятностям Р (0,01 и 0,99) и заданному числу степеней свободы 
находим 
.
Доверительный интервал дисперсии, соответствующий доверительной вероятности , определяется по формуле (10):
.
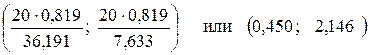Контрольные вопросы
1. Какие оценки параметров называются точечными?
2. Что такое состоятельность, эффективность и несмещенность точечных оценок?
3. В чем состоит метод моментов определения точечных оценок?
4. Что такое доверительный интервал, доверительная вероятность?
5. Что такое 
-распределение?
6. Чему равны параметры -распределения?
7. Охарактеризуйте распределение Стьюдента.
8. Почему рассмотренный способ построения доверительных интервалов применим только при выборке из нормальной генеральной совокупности?
Дата добавления: 2014-12-23; просмотров: 181; Мы поможем в написании вашей работы!; Нарушение авторских прав |