Примеры. Пусть выдвинуты гипотезы о распределении генеральной совокупности:

Пусть выдвинуты гипотезы о распределении генеральной совокупности:

1) по показательному закону

где - оценка параметра показательного закона распределения по выборке; . Здесь 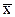- оценка математического ожидания;

2) по нормальному закону ,

где 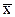- оценка математического ожидания, - оценка дисперсии по выборке. - оценка среднего квадратичного; - функция Лапласа (табл. А1);

3) по закону Релея ,

где 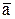- оценка параметра закона Релея по выборке : ;

4) по равномерному закону ,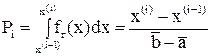

где 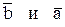- оценки крайних значений выборки, которые находятся из системы .

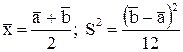Случайная величина , независимо от вида закона распределения генеральной совокупности, при достаточно больших имеет распределение с числом степеней свободы , где 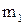- число интервалов, r – число параметров распределения, определенных по выборке.

Задаваясь уровнем значимости , по таблице А2 определим критическое значение , такое, что . При больших распределено асимптотически нормально и можно пользоваться таблицами нормального закона. Если 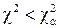, то выдвинутая гипотеза о виде закона распределения генеральной совокупности не отвергается на уровне значимости 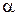(гипотеза не противоречит опытным данным), если же , то гипотеза отвергается на уровне значимости .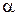

Замечание. Критерий Пирсона обладает большей мощностью, если интервалы содержат примерно равное число элементов, при этом длины интервалов не обязательно должны быть равными. Поэтому при использовании критерия Пирсона нужно произвести новое разбиение данной выборки на интервалы, содержащие примерно равное число элементов.

Замечание.Все расчеты вести с тем количеством знаков, с каким даны значе-

ния случайной величины (можно добавить один дополнительный знак).