Построение доверительного интервала математического ожидания

Полученные на первом этапе оценки 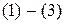называются точечнымии являются случайными величинами, изменяющимися от выборки к выборке. Использование точечных оценок, построенных по выборкам малого объема (n ~ 10), может привести к существенным ошибкам. Например, среднее арифметическое 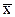, как оценка математического ожидания 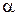, имеет дисперсию . При больших n дисперсия оценки мала, и реализация оценки 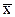весьма тесно концентрируется около своего математического ожидания, равного 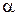. При малых объемах выборки дисперсия оценки 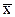может быть большой.

В случае использования точечных оценок, построенных по выборкам малого объема, необходимо указать, с какой степенью уверенности можно говорить о том, что отклонение оценки а* от оцениваемого параметра ане превзойдет определенную величину.

По заданной вероятности 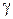(как правило, 0,9; 0,95; 0,99) определим число 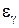, такое, что 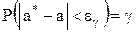, или, что то же самое,

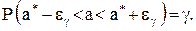(4)

Интервал 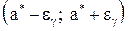, с вероятностью 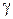содержащий истинное значение оцениваемого параметра 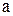, называется доверительным интервалом; границы его - случайные величины. Вероятность 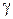называется доверительной вероятностью.

Доверительный интервал может быть несимметричным относительно оцениваемого параметра.

В случае выборки из нормальной генеральной совокупности оценка 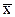имеет

нормальное распределение с параметрами 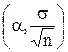, где 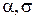- параметры нормаль-

ной генеральной совокупности. Если параметр известен, то

, (5)

где 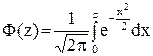- функция Лапласа. Из равенства

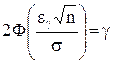, (6)

используя таблицу А1, можно определить 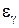. Интервал 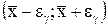является доверительным интервалом для математического ожидания, соответствующим доверительной вероятности .

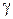Если параметр не известен, то простая замена этого параметра в формуле (5) его оценкой в случае малой выборки может привести к существенным ошибкам.

В этом случае можно воспользоваться случайной величиной 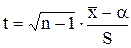, где 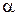- математическое ожидание генеральной совокупности, 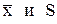- оценки параметров нормальной генеральной совокупности. В курсе математической статистики доказывается, что случайная величина t в выборке из нормальной генеральной совокупности имеет распределение Стьюдента (t - распределение) с (n-1) степенями свободы, распределение, не зависящее от параметров генеральной совокупности.

Пусть число 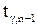таково, что 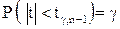, (7)

где 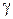– заданная доверительная вероятность.

Равенство (7) означает, что 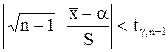с вероятностью 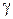. Последнее

неравенство эквивалентно следующему:

. (8)

Следовательно, интервал 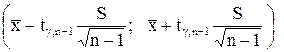является доверительным интервалом математического ожидания, соответствующим доверительной вероятности .

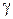Значения 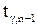, зависящие от 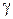и числа степеней свободы 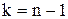, могут быть определены по таблице А3.