
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Построение доверительного интервала дисперсии
В курсе математической статистики доказано, что в выборке из нормальной ге-
неральной совокупности с параметрами  случайная величина
случайная величина  ,
,
где  – оценка неизвестной дисперсии, равная
– оценка неизвестной дисперсии, равная  , имеет распределение
, имеет распределение
 с n степенями свободы. Если параметр
с n степенями свободы. Если параметр 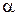 неизвестен, то в выражении
неизвестен, то в выражении  можно заменить
можно заменить 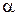 на его оценку
на его оценку 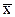 ; в этом случае случайная величина
; в этом случае случайная величина  также имеет распределение
также имеет распределение  , но уже с
, но уже с 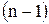 , а не с n степенями свободы.
, а не с n степенями свободы.
Пусть числа  выбраны таким образом, что
выбраны таким образом, что
 , (9)
, (9)
где 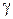 – заданная доверительная вероятность.
– заданная доверительная вероятность.
Равенство (9) означает, что  c вероятностью
c вероятностью 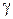 . Последнее двойное неравенство эквивалентно следующему:
. Последнее двойное неравенство эквивалентно следующему:
 . (10)
. (10)
Следовательно,  является доверительным интервалом дисперсии, соответствующим доверительной вероятности
является доверительным интервалом дисперсии, соответствующим доверительной вероятности 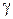 .
.
Однако по заданной вероятности 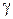 можно построить множество доверительных интервалов для дисперсии. Принято
можно построить множество доверительных интервалов для дисперсии. Принято  выбирать так, чтобы вероятности
выбирать так, чтобы вероятности  были равны и равны
были равны и равны  (рис. 1).
(рис. 1).
Соответствующие значения  могут быть определены по таблице А2.
могут быть определены по таблице А2.
Замечание. При больших объемах выборок можно воспользоваться тем, что рассмотренные оценки математического ожидания и дисперсии распределены
асимптотически нормально.


|

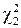 x
x
Дата добавления: 2014-12-23; просмотров: 290; Мы поможем в написании вашей работы!; Нарушение авторских прав |
 - распределения с
- распределения с  степенями свободы
степенями свободы 