Построение линии регрессии

Связь зависимой переменной с одной или несколькими независимыми пере-

менными представляют в виде уравнения регрессии .

Построение уравнения регрессии предполагает решение двух задач:

а) выбор независимых переменных, существенно влияющих на зависимую величину, и определение вида уравнения регрессии;

б) оценивание параметров (коэффициентов) уравнения.

Пусть для одной независимой переменной по расположению точек 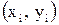на плоскости выдвинута гипотеза о линейной зависимости между переменными , т. е. 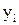- исход 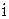-ого опыта, можно представить в виде:

, (1)

где - число опытов, 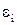- случайные добавки, при учете которых любой индивидуальный 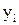получает возможность не попасть на линию регрессии, - неизвестные параметры. Предполагается, что 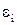распределены нормально с параметрами и независимы. Начнем с предположения, что модель установлена, но на последующих стадиях будем проверять, так ли это на самом деле. Модель (1) линейна относительно неизвестных параметров, относительно неизвестной функции модель (1) первого порядка.

В соответствии с методом наименьших квадратов оценки параметров находятся из условия обращения в минимум величины

(2)

Дифференцируя равенство (2) по и приравнивая полученные частные производные нулю, для нахождения оценок 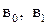получим так называемую нормальную систему:

(3)

Решив систему (3), найдем оценки неизвестных параметров :

(4)

Замечание. Для линейной модели второго порядка

,

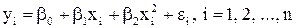нормальная система для нахождения оценок неизвестных параметров будет иметь вид

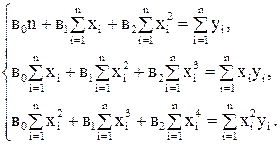(5)

Если ввести следующие обозначения

то система (5) может быть записана в виде

. (6)

Для модели , , где - значение –й независимой переменной , в 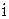-м опыте, нормальная система также будет иметь вид (6), если

.