Построение доверительных интервалов для коэффициентов регрессии

Для построения доверительных интервалов для 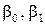необходимо знать законы распределения их оценок 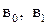. Если 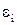распределены нормально с параметрами и независимы, то случайные величины также распределены нормально и независимы. После преобразования формул (4) получим

,

Оценки 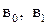также имеют нормальное распределение, как линейные комбинации нормально распределенных случайных величин. Можно показать, что

(7)

где - ошибка опыта. Случайная величина 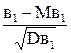распределена нормально с параметрами . Но неизвестно, поэтому в (7) заменим его оценкой . Тогда

. (8)

Замена неслучайной величины ее оценкой, являющейся случайной величиной, приводит к тому, что величина только асимптотически нормальна . Для малых величина имеет 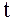-распределение, число степеней свободы определяется способом нахождения , точнее способом нахождения .

Лучшим способом является нахождение 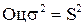по параллельным опытам (опытам, поставленным в одной точке). В этом случае

, (9)

где - -е значение в точке 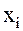, – число повторных наблюдений в точке 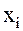, - число точек, в которых проводятся повторные опыты.

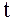Тогда величина имеет -распределение с степенями свободы. Доверительный интервал для , соответствующий доверительной вероятности 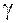, имеет вид

,

где - значение 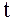, при котором .

Замечание. Если параллельных опытов нет, то оценка может быть найдена следующим образом. Пусть - предсказанное значение данного , когда определены, т. е. .

В качестве оценки может быть принято следующее отношение:

. (10)

Сумма имеет степени свободы, т. к. по данным испытаний определяются два коэффициента. Величина в этом случае имеет -распределение с степенями свободы.

Доверительный интервал для можно использовать для проверки гипотезы . Если доверительный интервал, соответствующий доверительной вероятности 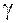, содержит значение , то гипотеза не отвергается на уровне значимости . В частности доверительный интервал может быть использован для проверки гипотезы 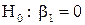. Если гипотеза отвергается, то параметр называется значимым. Аналогичными рассуждениями можно получить доверительный интервал для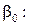

,

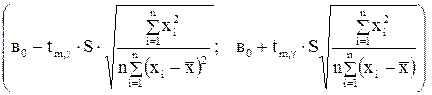где определяется способом нахождения .

Интерес для практики представляет доверительный интервал для линии регрессии. Для его построения необходимо знать оценку дисперсии . 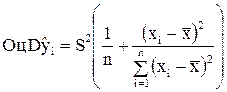, где определяется по формуле (9) или (10).

Доверительный интервал для имеет вид

. (11)

Доверительная зона (11) определяет местоположение линии регрессии, а не воз-

можных значений зависимой переменной. Доверительный интервал для значений определяется по формулам

.