Проверка согласия теоретического и статистического распределений

При построении гистограммы была выдвинута гипотеза о законе распределения генеральной совокупности. Назовем этот закон распределения теоретическим. Проверим его согласие с распределением выборки.

Сущность проверки статистической гипотезы заключается в том, чтобы установить, согласуются или нет данные наблюдения и выдвинутая гипотеза, можно ли расхождения между гипотезой и результатом выборочных наблюдений отнести за счет случайной погрешности, обусловленной механизмом случайного отбора. При этом критерии в задачах проверки гипотез о параметрах распределения называют критериями значимости, а в задачах проверки гипотез о законах распределения – критериями согласия.

Идея проверки статистической гипотезы состоит в следующем. Пусть - выдвинутая гипотеза, которую назовем основной, противопоставляя ее множеству альтернативных гипотез. Для проверки основной гипотезы проводится опыт, результатом которого является величина , скалярная мера близости между гипотетическим и эмпирическим распределениями или между гипотетической и эмпирической характеристиками распределения. представляет собой одномерную величину, значения которой изменяются от опыта к опыту. Закон распределения предполагается известным. По заданному область значений можно разбить на две области: . Область определяется из условия 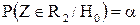и называется критической областью гипотезы на уровне значимости 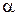. Таким образом, при условии справедливости гипотезы попадание величины в критическую область есть событие маловероятное, практически невозможное. Процедура проверки гипотезы заключается в следующем: по заданному уровню значимости 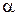определяются , затем проводится опыт. Если его результат , т. е. произошло событие, практически невозможное при условии справедливости гипотезы , то гипотеза отвергается на уровне значимости 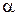. Если , т. е. , то гипотеза не отвергается на уровне значимости 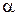. Стандартным значением для уровня значимости является одно из следующих значений: 0,05; 0,01; 0,001. Величина Z называется критериемпроверки гипотезы .

Очевидно, что при такой проверке правильная гипотеза может быть отвергнута.

Ошибка, заключающаяся в том, что отвергается верная гипотеза, называется ошибкой первого рода. Вероятность такой ошибки равна 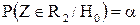. Выбор малого 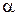гарантирует, что ошибка первого рода будет совершаться редко.

Возможна еще ошибка второго рода, состоящая в том, что гипотеза ,будучиневерной, не отвергается. Вероятность ошибки второго рода равна

. Величина

называется мощностью критерия при заданном 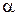. Для уменьшения вероятности ошибки второго рода или, что то же самое, для увеличения мощности критерия, вероятность должна быть возможно большей.

Таким образом, при выборе критической области будем руководствоваться следующими соображениями:

, . (3)

Процесс проверки статистической гипотезы сводится к следующему:

- выдвигается основная гипотеза и множество альтернативных гипотез ;

- выбирается критерий, представляющий собой некоторую меру близости между гипотетическим и эмпирическим распределениями или между гипотетической и эмпирической характеристиками распределения;

- критерий выбирается так, чтобы его распределение было известно;

- назначается уровень значимости 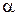и определяется критическая область ;

- производится опыт и по данным опыта (выборочным наблюдениям) вычисля-

ется значение критерия ;

- если 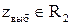, то гипотеза отвергается, если , то гипотеза не отвергается на уровне значимости .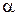

Из большого числа различных критериев чаще других используется критерий согласия , предложенный К. Пирсоном. В этом критерии в качестве меры расхождения теоретического и статистического распределений выбирается величина , определяемая равенством

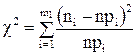, (4)

где n – объем выборки; 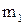– число интервалов, на которые разбита выборка;

–число элементов выборки, попавших в 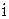-й интервал; 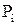– теоретическая вероятность попадания значений случайной величины в 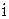-й интервал.

Вероятность 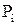определяется в согласии с теоретическим законом распределения

, (5)

или , (6)

где - границы 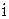–го интервала.