Краткая теоретическая часть.

Сущность геометрического определения вероятности.

Еще в самом начале развития теории вероятностей была замечена недостаточность «классического» определения вероятности, основанного на рассмотрении конечной группы равновероятных событий. Уже тогда частные примеры привели к некоторому видоизменению этого определения и построению понятия вероятности также для случаев, когда мыслимо бесконечное множество исходов. При этом по-прежнему основную роль играло понятие «равновероятности» некоторых событий.

Общая задача, которая ставилась и привела к расширению понятия вероятности, может быть сформулирована следующим способом.

Пусть, например, на плоскости имеется некоторая область G и в ней содержится другая область g с квадрируемой границей. В область G наудачу бросается точка и спрашивается, чему равна вероятность того, что точка попадет в область g. При этом выражению «точка бросается наудачу в область G» придается следующий смысл: брошенная точка может попасть в любую точку области G, вероятность попасть в какую-либо часть области G пропорциональна мере этой части (длине, площади и т. д.) и не зависит от ее расположения и формы.

Таким образом, по определению, вероятность попадания в область g при бросании наудачу точки в область G равна .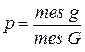

Примеры.

Рассмотрим несколько примеров.

Пример 1. Задача о встрече.

Два лица А и В условились Встретиться в определенном месте между 12 часами и часом. Пришедший первым ждет другого в течение 20 минут, после чего уходит. Чему равна вероятность встречи лиц А и В, если приход каждого из них в течение указанного часа может произойти наудачу и моменты прихода независимы.

Решение.

Обозначим моменты прихода лица А через х и лица В через у. Для того чтобы встреча произошла, необходимо и достаточно, чтобы .

Будем изображать хOу как декартовы координаты на плоскости; в качестве единицы масштаба выберем минуту. Всевозможные исходы изобразятся точками квадрата со сторонами 60; благоприятствующие встрече — расположатся в заштрихованной области (рис. 2.1).

Искомая вероятность равна отно­шению площади заштрихованной фигуры к площади всего квадрата:

Пример 2. Задача Бюффона.

Плоскость разграфлена параллельными прямыми, отстоящими друг от друга на расстоянии 2а. На плоскость наудачу бросается игла длины 2l(l≤a). Найти вероятность того, что игла пересечет какую-нибудь прямую.

Решение.

Обозначим через х расстояние от центра до ближайшей параллели и через —угол, составленный иглой с этой параллелью. Величины х и полностью определяют положение иглы. Всевозможные положения иглы определяются точками прямоугольника со сторонами a и . Из рис. 2.2. видно, что для пересечения иглы с параллелью необходимо и достаточно, чтобы .

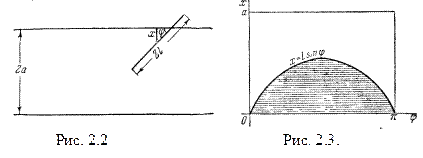
Искомая вероятность в силу сделанных предположений равна отношению площади заштрихованной на рис. 2.3. области к площади прямоугольника

Заметим, что задача Бюффона являлась исходным пунктом для решения некоторых проблем теории стрельбы, учитывающих размеры снаряда

Тест

1. Применимо ли геометрическое определение вероятности, если число исходов опыта бесконечно?

а) Да

б) Нет

2. Пусть на плоскости имеется некоторая область G с квадрируемой границей и в ней содержится подобласть g. В область G наудачу бросается точка. Определить, какова вероятность того, что точка попадет в подобласть g. Выберите условия, выполнение которых необходимо для того, чтобы эту задачу можно было бы решить с использованием геометрического определения вероятности.

а) Точка может попасть в любую точку области G с равной вероятностью

б) Вероятность попадания брошенной точки в каждую точку области G определяется по некоторому закону и необязательно одинакова

в) Вероятность попадания точки в подобласть g зависит от ее формы и расположения

г) Вероятность попадания точки в подобласть g не зависит от ее формы и расположения

д) Вероятность попадания точки в какую-либо часть области G пропорциональна мере этой части (длине, площади и т.д.)

е) Вероятность попадания точки в какую-либо часть области G не пропорциональна мере этой части

3. Если выполняются все необходимые условия для применения геометрического определения вероятности, то вероятность попадания в подобласть g при бросании наудачу точки в область G равна:

а) P = mes g / mes G

б) P = mes G / mes g

в) P = 1 / mes G

г) P = 1 / mes g

д) P = mes G - mes g

е) P = mes g mes G

4. В чем заключается основное преимущество геометрического определения вероятности над классическим?

а) Наглядность

б) Возможность применения в случае бесконечного числа исходов опыта

в) Нет необходимости в том, чтобы исходы опыта были равновозможны

г) Никаких преимуществ нет, эти определения полностью эквивалентны

5. Какую из следующих задач нельзя решить с использованием геометрического определения вероятности?

а) В большой лекционной аудитории объема V летает комар. Один из студентов выпустил струю газа инсектицида из баллончика, в результате чего образовалось облако объема v. Какова вероятность того, что комар попадет в это облако, если нахождение его в любой точке аудитории равновероятно и вероятность попадания в любую подобласть аудитории пропорциональна размерам этой подобласти.

б) В лужу площади S падает камушек. Определить вероятность того, что камушек упадет на монетку, лежащую на дне, если и камушек, и монетка рассматриваются как материальные точки, расположение монетки в луже известно заранее, а попадание камушка в любое место лужи равновозможно.

в) В круг радиуса R помещен меньший круг радиуса r.Определить вероятность того, что точка, наудачу брошенная в большой круг, попадет также и в малый круг. Предполагается, что вероятность попадания точки в круг пропорциональна площади круга и не зависит от его расположения.

г) Все задачи можно решать с использованием геометрического определения вероятности.

д) Ни к одной из перечисленных задач геометрическое определение неприменимо.