Теорема Ляпунова.

Пусть - независи­мые и одинаково распределенные случайные величины с числовыми характеристиками

(10.2.1)

Тогда

(10.2.2)

Доказательство. Прежде всего отметим, что выражение вида (10.2.2) совпадает с в выражениях (10.1.2), если считать выполненными условия (10.2.1). Поэтому доказательство должно сводиться к установлению сходимости (10.1.7).

Далее, в выражение (10.2.2) для входят только центрированные составляющие , случайных величин , поэтому доказательство можно проводить, полагая в (10.2.2) , т.е. при условиях

(10.2.3)

где - независимые и одинаково распределенные. Поскольку , одинаково распределены, то их характеристические функции совпадают:

(10.2.4)

Учитывая независимость , получим следующее выражение характеристической функции случайной величины :

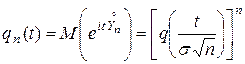
Отсюда следует

(10.2.5)

Разлагая в ряд по степеням правую часть уравнения (10.2.5) при достаточно больших п получим с учетом теоремы о дифференцируемости характеристических функций

Отсюда найдем

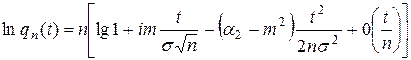
В силу условия 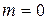и формулы получим

Теперь можно записать

Отсюда следует требуемое

К числу простейших форм центральной предельной теоремы относится также теорема Лапласа.