Сходимость последовательностей случайных величин.

Пусть на вероятностном пространстве 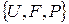определены случайные величины со значениями .

Определение 1. Последовательность 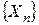сходится по вероятности (п.в) к величине X, если

(9.1.1)

Обозначим сходимость 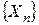к X по вероятности символом .

Определение 2. Последовательность 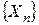сходится к X почти наверное (п.н) (с вероятностью единица), если

(9.1.2)

Обозначим эту сходимость символом .

Определение 3. Говорят, последовательность сходится к X в среднеквадратическом (с.к.), если

(9.1.3)

Обозначим эту сходимость символом .

Определение 4. Последовательность сходится к X по распределению (п.р) с обозначением , если

(9.1.4)

Здесь F_n,F- функции распределения X_n и X, причем сходимость {F_n} к F подразумевается для всех x, за исключением, может быть, точек разрыва F.

Сходимости {X_n} к X, введенные определениями 1-4, связаны между собою отношениями, показанными на рис. 9.1.1.

Рис. 9.1.1.