Теоремы о дисперсии случайной величины.

Теорема 6. Неслучайную величину можно выносить за знак дисперсии, возводя ее в квадрат.

Если с — неслучайная величина, а X — случайная, то

(7.2.1)

Доказательство. По определению дисперсии

Следствие

(7.2.2)

т. е. неслучайную величину можно выносить за знак среднеквадратического отклонения ее абсолютным значением. Доказательство получим, извлекая корень квадратный из формулы (7.2.1) и учиты­вая, что среднеквадратическое положительная величина.

Теорема 7. Дисперсия неслучайной величины равна нулю

Если с — неслучайная величина, то

, тогда

(7.2.3)

Теорема 8.Дисперсия суммы двух случайных величин равна сумме их диспер­сий плюс удвоенный корреляционный момент:

(7.2.4)

Доказательство. Обозначим

(7.2.5)

По теореме сложения математических ожиданий

(7.2.6)

Перейдем от случайных величин X,Y,Z к соответствующим центрированным величинам X,Y,Z. Вычитая почленно из равенства (7.2.5) равенство (7.2.6), имеем:

По определению дисперсии

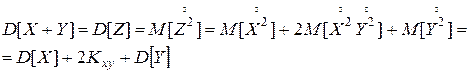
что и требовалось доказать.

Формула (7.2.4) для дисперсии суммы может быть обобщена на любое число слагаемых:

(7.2.7)

где Кij — корреляционный момент величин X_i , X_j, знак i<j под суммой обозначает, что суммирование распространяется на все воз­можные попарные сочетания случайных величин (X₁ ,Х₂.....,Х_n).

Доказательство аналогично предыдущему и вытекает из формулы для квадрата многочлена.

Формула (7.2.7) может быть записана еще в другом виде:

(7.2.8)

где двойная сумма распространяется на все элементы корреляционной матрицы системы величин (Х₁,Х₂,....Х_n), содержащей как корреляционные моменты, так и дисперсии.

Если все случайные величины (Х₁,Х₂,...,Х_п), входящие в систему, некоррелированы (т. е. Кij = 0 при i 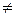j). формула (7.2.7) принимает вид:

(7.2.9)

т.е. дисперсия суммы некоррелированных случайных величин равна сумме дисперсий слагаемых.

Это положение известно под названием теоремы сложения дисперсий.

Теорема 9. Дисперсия линейной конбинации случайных величин определяется соотношением

(7.2.10)

где К_ij— корреляционный момент величин X_i, X_j.

Доказательство. Введем обозначение:

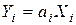
Тогда

(7.2.11)

Применяя к правой части выражения (7.2.11) формулу (7.2.7) для дисперсии суммы и учитывая, что D[b] = 0, получим:

(7.2.12)

где — корреляционный момент величин Y_i, Y_j.

Вычислим этот момент. Имеем:

аналогично

Отсюда

Подставляя это выражение в (7.2.12), приходим к формуле (7.2.10).

В частном случае, когда все величины (Х₁,Х₂,...,Х_n) некоррелированные, формула (7.2.10) принимает вид:

(7.2.13)

т.е. дисперсия линейной функции некоррелированных случайных величин равна сумме произведений квадратов коэффициен­тов на дисперсии соответствующих аргументов).

Теорема 10. Дисперсия произведения независимых случайных величин определяется соотношением

(7.2.14)

Доказательство. Обозначим XY=Z. По определению дисперсии

Так как величины X, Y независимы, m_z = m_xm_y и

При независимых X, У величины Х², Y² тоже независимы следовательно,

и

(7.2.15)

Но М[X²] есть не что иное, как второй начальный момент величины X, и, следовательно, выражается через дисперсию:

(7.2.16)

аналогично

(7.2.17)

Подставляя выражения (7.2.16) и (7.2.17) в формулу (7.2.15) и приводя подобные члены, приходим к формуле (7.2.14).

В случае, когда перемножаются центрированные случайные величины (величины с математическими ожиданиями, равными нулю), формула (7.2.14) принимает вид:

(7.2.18)

т.е. дисперсия произведения независимых центрированных случайных величин равна произведению их дисперсий.