Предельные теоремы для характеристических функций.

Важнейшими с точки зрения приложений характеристических функций к выводу асимптотических формул теории вероятностей являются две предельные теоремы — прямая и обратная. Эти теоремы устанавливают, что соответствие, существующее между функциями распределения и характеристическими функциями, не только взаимно однозначно, но и непрерывно. Формулировки теорем приведем без доказательства.

Прямая предельная теорема. Если последовательность функций распределения

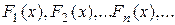
сходится в основном к функции распределения F(х), то последовательность характеристических функций

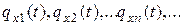
сходится к характеристической функции q_x(t). Эта сходимость равномерна в каждом конечном интервале t.

Обратная предельная теорема. Если последовательность характеристических функций

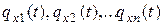
сходится к непрерывной функции q_x(t), то последовательность функций распределения

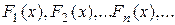
сходится в основном к некоторой функции распределения F(x).

Заметим, что условия теоремы выполнены в каждом из двух следующих случаев:

1) Последовательность характеристических функций 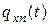сходится к некоторой функции q_x(t) равномерно в каждом конечном интервале t.

2) Последовательность характеристических функций 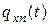сходится к характеристической функции q_x(t).