Распределение произведения.

Пусть , где и — скалярные случайные величины с совместной плотностью распределения 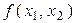. Найдем распределение Y.

(6.4.1)

На рис. событие показано штриховкой. Теперь очевидно, что

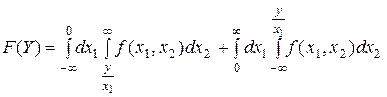
	(6.4.2)
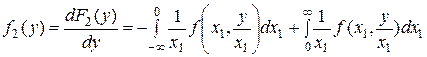
	(6.4.3)

Распределение квадрата случайной величины.

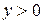Пусть ; X — непрерыная случайная величина с плотностью . Найдем . Если , то и . В том случае, когда получаем:

	(6.5.1)
	(6.5.2)

В частном случае, когда , имеем:

(6.5.3)

Если при этом , , то

(6.5.4)

Распределение частного.

Пусть ; X — непрерывная случайная величина с плотностью 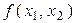. Найдем .

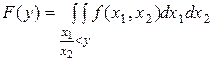
(6.6.1)

На рис. 6.6.1 видно, что событие — изображают заштрихованные области. Поэтому

	(6.6.2)
	(6.6.3)

Если ; ; 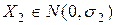независимы, то легко получить:

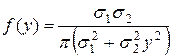
(6.6.4)

Распределение (6.6.4) носит имя Коши. Оказывается, это распределение не имеет математического ожидания и дисперсии.