Система произвольного числа случайных величин (случайные вектора).

Определение 1. Функцией распределения системы п случайных величин называется вероятность совместного выполнения п неравенств вида , то есть :

(5.7.1)

Определение 2. Плотностью распределения системы п непрерывных случайных величин называется n-я смешанная частная производная функции 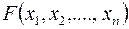, взятая один раз по каждому аргументу:

(5.7.2)

Зная закон распределения системы, можно определить законы распределения отдельных величин, входящих в систему. Функция распределения каждой из величин, входящих в систему, получится, если в функции распределения системы положить все остальные аргументы равными :

(5.7.3)

Если выделить из системы величин подсистему , то функция распределения этой подсистемы определяется по формуле

(5.7.4)

Плотность распределения каждой из величин, входящих в систему, получится, если плотность распределения системы проинтегрировать в бесконечных пределах по всем остальным аргументам:

(5.7.5)

Плотность распределения подсистемы , выделенной из системы , равна:

(5.7.6)

Определение 3. Условным законом распределения подсистемы называется ее закон распределения, вычисленный при условии, что остальные величины приняли значения .

Условная плотность распределения ее может быть вычислена по формуле:

(5.7.7)

Случайные величины называются независимыми, если закон распределения каждой частной подсистемы, выделенной из системы , не зависит от того, какие значения при­няли остальные случайные величины.

Плотность распределения системы независимых случайных вели­чин равна произведению плотностей распределения отдельных вели­чин, входящих в систему:

(5.7.8)

Вероятность попадания случайной точки в пре­делы n-мерной области D выражается n-кратным интегралом:

(5.7.9)

Эта формула по существу является основной формулой для вычисления вероятностей событий, не сводящихся к схеме случаев.