Зависимые и независимые случайные величины.

При изучении систем случайных величин всегда следует обращать внимание на степень и характер их зависимости. Эта зависимость может быть более или менее тесной.

Понятие о независимых случайных величинах — одно из важных понятий теории вероятностей.

Определение 1. Случайная величина Y называется независимой от случайной ве­личины X, если закон распределения величины Y не зависит от того, какое значение приняла величина X.

Для непрерывных случайных величин условие независимости Y от X может быть записано в виде:

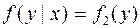
(5.5.1)

Напротив, в случае, если Y зависит от X, то

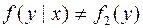
(5.5.2)

Докажем, что зависимость или независимость случайных ве­личин всегда взаимны: если величина Y не зависит от X, то и ве­личина X не зависит от Y.

Действительно, пусть Y не зависит от X, тогда

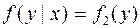
Плотность совместного распределения согласно (5.4.5) и (5.4.6) можно записать

(5.5.3)

откуда, получим:

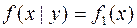
что и требовалось доказать.

Так как зависимость и независимость случайных величин всегда взаимны, можно дать новое определение независимых случайных величин.

Определение 2. Случайные величины X и Y называются независимыми, если закон распределения каждой из них не зависит от того, какое значение приняла другая. В противном случае величины X и Y называются зависимыми.

Для независимых непрерывных случайных величин теорема умно­жения законов распределения принимает вид:

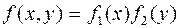
(5.5.4)

т.е. плотность распределения системы независимых случайных величин равна произведению плотностей распределения от­дельных величин, входящих в систему.

Остановимся, несколько подробнее на важных понятиях о «зави­симости» и «независимости» случайных величин.

Понятие «зависимости» случайных величин, которым мы пользу­емся в теории вероятностей, несколько отличается от обычного по­нятия «зависимости» величин, которым мы оперируем в математике. Действительно, обычно под «зависимостью» величин подразумевают только один тип зависимости—полную, жесткую, так называемую функциональную зависимость. Две величины X и Y называются функционально зависимыми, если, зная значение одной из них, можно точно указать значение другой.

В теории вероятностей мы встречаемся с другим, более общим, типом зависимости — с вероятностной или «стохастической» зави­симостью. Если величина Y связана с величиной X вероятностной зависимостью, то, зная значение X, нельзя указать точно значение Y, а можно указать только ее закон распределения, зависящий от того, какое значение приняла величина X.

Вероятностная зависимость между случайными величинами очень часто встречается на практике. Если случайные величины X и Y находятся в вероятностной зависимости, это не означает, что с из­менением величины X величина Y изменяется вполне определенным образом; это лишь означает, что с изменением величины X величина Y имеет тенденцию также изменяться (например, возрастать или убывать при возрастании X).

Рассмотрим, например, две такие случайные величины: X — рост наугад взятого человека, Y — его вес. Очевидно, величины X и Y находятся в определенной вероятностной зависимости; она выражается в том, что в общем люди с большим ростом имеют больший вес.