Вероятность попадания случайной величины, подчиненной нормальному закону, на заданный участок. Нормальная функция распределения.

Во многих задачах, связанных с нормально распределенными случайными величинами, приходится определять вероятность попадания случайной величины X на участок от 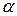до 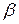. Для вычисления этой вероятности воспользуемся общей формулой

(4.6.12)

где F(х) — функция распределения случайной величины X.

Найдем функцию распределения F(х) случайной величины X распределенной по нормальному закону с параметрами т, .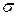

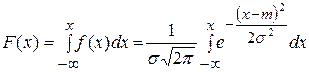
(4.6.13)

Сделаем в интеграле замену переменной и приведем его к виду:

(4.6.14)

Данный интеграл не выражается через элементарные функции, но его можно вычислить через специальную функцию, выражающую определенный интеграл от выражения или (так называемый интеграл вероятностей), для которого составлены таблицы. Существует много разновидностей таких функций, например:

	(4.6.15)

и т.д.

Нетрудно видеть, что эта функция представляет собой не что иное, как функцию распределения для нормально распределенной случайной величины с параметрами m=0, 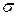=1.

Условимся называть функцию Ф*(х) нормальной функцией распределения. Очевидно, что

(4.6.16)

Теперь найдем вероятность попадания случайной величины Х на участок от 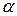до .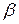

(4.6.17)

Таким образом, мы выразили вероятность попадания на интервал случайной величины X, распределенной по нормальному закону с любыми параметрами, через стандартную функцию распределения Ф*(х), соответствующую простейшему нормальному закону с параметрами 0,1.

Как и всякая функция распределения, функция Ф*(х) обладает свойствами:

1. Ф*( 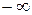)= 0.

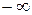2. Ф*( )= 1.

3. Ф*(x) - неубывающая функция.

Кроме того, из симметричности нормального распределения с параметрами m=0, 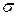=1 относительно начала координат следует, что

(4.6.18)

На практике часто встречается задача вычисления вероятности попадания нормально распределенной случайной величины на участок, симметричный относительно центра рассеивания т. Рассмотрим такой участок длины 2l (рис. 4.6.4). Вычислим вероятность попадания на этот участок:

(4.6.19)

Учитывая свойство (4.6.18) функции Ф*(х) и придавая левой части формулы (4.6.19) более компактный вид, получим формулу для вероятности попадания случайной величины, распределенной по нормальному закону, на участок, симметричный относительно центра рассеивания:

(4.6.20)

Решим следующую задачу. Отложим от центра рассеивания т последовательные отрезки длиной 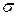(рис. 4.6.5) и вычислим вероятность попадания случайной величины Х в каждый из них. Так как кривая нормального закона симметрична, достаточно отложить такие отрезки только в одну сторону. По формуле (4.6.17) находим:

Как видно из этих данных, вероятности попадания на каждый из следующих отрезков (пятый, шестой и т. д.) с точностью до 0,001 равны нулю.

Округляя вероятности попадания в отрезки до 0,01 (до 1%) получим три числа, которые легко запомнить:

0,34; 0,14; 0,01.

Сумма этих трех значений близка 0,5. Это значит, что для нор­мально распределенной случайной величины все рассеивание (с точ­ностью до долей процента) укладывается на участке т ± 3 .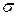

Это позволяет, зная среднеквадратическое отклонение и математическое ожидание случайной величины, ориентировочно указать интервал ее практически возможных значений. Такой способ оценки диапазона возможных значений случайной величины известен в математической статистике под названием «правило трех сигма».