Моменты нормального распределения.

Выше мы доказали, что математическое ожидание случайной величины, подчиненной нормальному закону (4.6.1), равно т, а среднеквадратическое отклонение равно .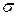

Выведем общие формулы для центральных моментов любого порядка.

По определению:

(4.6.5)

Делая замену переменной

получим:

(4.6.6)

проинтегрируем по частям, получим

(4.6.7)

Имея в виду, что первый член внутри скобок равен нулю, получим:

Из формулы (4.6.6) имеем следующее выражение для :

(4.6.8)

следовательно

(4.6.9)

Формула (4.6.9) представляет собой простое рекуррентное соотношение, позволяющее выражать моменты высших порядков через моменты низших порядков. Пользуясь этой формулой и имея в виду, что и 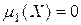, можно вычислить центральные моменты всех порядков. Так как 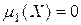, то из формулы (4.6.9) следует, что все нечетные моменты нормального распределения равны нулю.

Для четных s из формулы (4.6.9) вытекают следующие выражения для последовательности моментов:

; ;

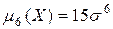
Общая формула для момента s-го порядка при любом четном s имеет вид:

(4.6.10)

где под символам (s—1)!! понимается произведение всех нечетных чисел от 1 до s-1.

Так как для нормального закона 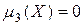, то асимметрия его также равна нулю:

(4.6.11)

Из выражения четвертого момента имеем:

, т. е. эксцесс нормального распределения равен нулю. Это и естественно, так как назначение эксцесса—характеризовать сравнительную крутость данного закона по сравнению с нормальным.